
【题目】如图,一次函数y=![]() ,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.
,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.

【答案】(-![]() )
)
【解析】
一次函数![]() ,的图象向下平移2个单位后得直线
,的图象向下平移2个单位后得直线![]() 在一次函数
在一次函数![]() 中,分别令x=0和y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,EF最小,由此可知P点坐标.
中,分别令x=0和y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,EF最小,由此可知P点坐标.

一次函数![]() ,的图象向下平移2个单位后得直线
,的图象向下平移2个单位后得直线![]() ,
,
由矩形的性质可知EF=OP,由垂线段最短可知当OP⊥AB时,则EF有最小值,
设P点的坐标(x,![]() ),
),
x=0和y=0,解相应方程A(-![]() ),B(
),B(![]() ),
),
AO=BO,
又OP⊥AB,
AP=BP,P为中点,
PE⊥![]() 轴点,PF⊥
轴点,PF⊥![]() 轴,
轴,
PF平行等于![]() AO,PE平行等于
AO,PE平行等于![]() BO,
BO,
PE=PF=![]() ,
,
此时EF最小,可知P点坐标(-![]() ).
).


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】2012年我国国民经济运行总体平稳,全年全国公共财政收入117210亿元,2008﹣2012年全国公共财政收入及其增长速度情况如图所示: 
(1)这五年中全国公共财政收入增长速度最高的年份是年;
(2)2012年的全国公共财政收入比2011年多亿元;
(3)这五年的全国公共财政收入增长速度的平均数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG , EH∥BD∥FG , 则四边形EFGH的周长是( ).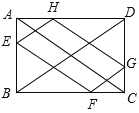
A.![]()
B.![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于D , 下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③ ![]() =
= ![]() ;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )
;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( ) 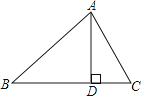
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AC , 点D在BC上,且DC=AC , ∠ACB的平分线CF交AD于F , 点E是AB的中点,连接EF . 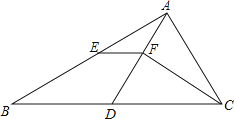
(1)求证:2EF=BD ,
(2)四边形BDFE的面积为6,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件,不能判定△ABC与△DEF相似的是( )
A.∠C=∠F=90°,∠A=55°,∠D=35°
B.∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9
C.∠C=∠F=90°, ![]() =
= ![]()
D.∠B=∠E=90°, ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
10 | 10 | 500 |
15 | 20 | 900 |
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com