
【题目】下列计算正确的是( )
A.2 ![]() +3
+3 ![]() =5
=5 ![]()
B.( ![]() )(1﹣
)(1﹣ ![]() )=1
)=1
C.(xy)﹣1( ![]() xy)2=
xy)2= ![]() xy
xy
D.﹣(﹣a)4÷a2=a2
【答案】C
【解析】解:∵2 ![]() +3
+3 ![]() =5
=5 ![]() , ∴选项A不符合题意;
, ∴选项A不符合题意;
∵( ![]() )(1﹣
)(1﹣ ![]() )=﹣1,
)=﹣1,
∴选项B不符合题意;
∵(xy)﹣1( ![]() xy)2=
xy)2= ![]() xy,
xy,
∴选项C符合题意;
∵﹣(﹣a)4÷a2=﹣a2 ,
∴选项D不符合题意.
故选:C.
【考点精析】关于本题考查的整数指数幂的运算性质和二次根式的混合运算,需要了解aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数);二次根式的混合运算与实数中的运算顺序一样,先乘方,再乘除,最后加减,有括号的先算括号里的(或先去括号)才能得出正确答案.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个(分别标有1号、2号),黄球1个,从中任意摸出1球是绿球的概率是 ![]() .
.
(1)试求口袋中绿球的个数;
(2)小明和小刚玩摸球游戏:第一次从口袋中任意摸出1球(不放回),第二次再摸出1球.两人约定游戏胜负规则如下:摸出“一绿一黄”,则小明赢;摸出“一红一黄”,则小刚赢.你认为这种游戏胜负规则公平吗?请用列表或画树状图的方法说明理由;若你认为不公平,请修改游戏胜负规则,使游戏变得公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )
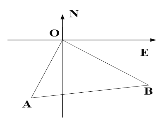
A. 南偏东30° B. 北偏东30° C. 南偏东 60° D. 南偏西 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A表示数a,点B表示数b,已知a、b满足![]() .
.
(1)求a、b的值;
(2)若在数轴上存在一点C,使得C到A的距离是C到B的距离的2倍,求点C表示的数;
(3)若小蚂蚁甲从点A处以1个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以2个单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒.求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明想探究函数![]() 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |
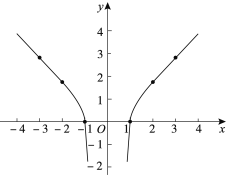
小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数![]() 的一条性质:_____________.
的一条性质:_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数1的点称为基准点,记作点![]() . 对于两个不同的M和N,若点M、点N到点
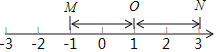
. 对于两个不同的M和N,若点M、点N到点![]() 的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数
的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数![]() ,点N表示数3,它们与基准点
,点N表示数3,它们与基准点![]() 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
① 若a=0,则b= ;若![]() ,则b= ;
,则b= ;
② 用含a的式子表示b,则b= ;
(2)对点A进行如下操作:先把点A表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到![]() ,
, ![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到![]() ,
, ![]() 为
为![]() 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到![]() ,
, ![]() ,…,
,…, ![]() .
. ![]() 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
, ![]() 为
为的基准变换点, 将数轴沿原点对折后
![]() 的落点为
的落点为![]() ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到![]() ,
, ![]() ,…,
,…, ![]() .若无论k为何值,
.若无论k为何值, ![]() 与
与![]() 两点间的距离都是4,则n= .
两点间的距离都是4,则n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N,当EN=MN时,则FM的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,sin∠EMP= ![]() .
.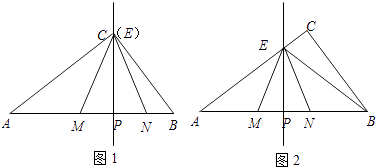
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A,C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出x的取值范围;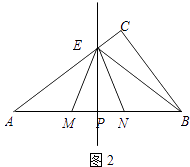
(3)若△AME∽△ENB,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com