课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案科目：初中数学 来源：新教材新学案 数学 八年级上册 题型：044
在同底数幂的除法法则中，am÷an＝am－n(m＞n)，当m＝n时，规定am÷an＝am－n＝a0＝1(a≠0)；若m＜n，我们还有什么样的发现呢？
计算：52÷56＝
；103÷105＝
．
于是就有：52÷56＝52－6＝5－4＝
；103÷105＝103－5＝10－2＝
．
因此规定a－p＝
(a≠0)，p是正整数．
你知道下列各数表示的数是多少吗？
(1)2×10－5；
(2)7－2；
(3)3.1×10－4；
(4)1.25×10－2．
查看答案和解析>>
科目：初中数学 来源：2013年江西省南昌市高级中等学校招生考试数学 题型：044
已知抛物线yn＝－(x－an)2＋an(n为正整数，且0＜a1＜a2＜…＜an)与x轴的交点为An－1(bn－1，0)和An(b，0)，当n＝1时，第1条抛物线y1＝－(x－a1)2＋a1与x轴的交点为A0(0，0)和A1(b1，0)，其他依次类推．
(1)求a1，b1的值及抛物线y2的解析式；
(2)抛物线y3的顶点坐标为(________，________)；
依次类推第n条抛物线yn的顶点坐标为(________，________)(用含n的式子表示)；
所有抛物线的顶点坐标满足的函数关系式是________；
(3)探究下列结论：
①若用An－1An表示第n条抛物线被x轴截得的线段长，直接写出A0A1的值，并求出An－1An；
②是否存在经过点A(2，0)的直线和所有抛物线都相交，且被每一条抛物线截得的线段长度都相等？若存在，直接写出直线的表达式；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源：2013年江西省高级中等学校招生考试数学 题型：044
已知抛物线抛物线yn＝－(x－an)2＋an(n为正整数，且0＜a1＜a2＜…＜an)与x轴的交点为An－1(bn－1，0)和An(bn，0)，当n＝1时，第1条抛物线y1＝－(x－a1)2＋a1与x轴的交点为A0(0，0)和A1(b1，0)，其他依此类推．
(1)求a1，b1的值及抛物线y2的解析式；
(2)抛物线y3的顶点坐标为(________，________)；
依此类推第n条抛物线yn的顶点坐标为(________，________)；
所有抛物线的顶点坐标满足的函数关系是________；
(3)探究下列结论：
①若用An－1An表示第n条抛物线被x轴截得得线段长，直接写出A0A1的值，并求出An－1An；
②是否存在经过点A(2，0)的直线和所有抛物线都相交，且被每一条抛物线截得得线段的长度都相等？若存在，直接写出直线的表达式；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源：2013-2014学年江苏省泰兴市九年级3月月考数学试卷（解析版） 题型：解答题
已知抛物线yn＝－(x－an)2＋an(n为正整数，且0＜a1＜a2＜…＜an)与x轴的交点为An－1(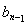
,0)和An(bn,0)．当n＝1时，第1条抛物线y1＝－(x－a1)2＋a1与x轴的交点为A0(0,0)和A1(b1,0)，其他依此类推．
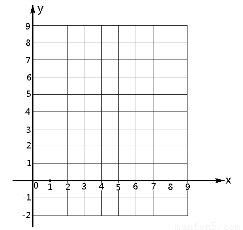
(1) 求a1、b1的值及抛物线y2的解析式；
(2) 抛物线y3的顶点坐标为(____，___)；依此类推第n条抛物线yn的顶点坐标为(_____，_____)(用含n的式子表示)；所有抛物线的顶点坐标满足的函数关系式是_____________；
(3) 探究下列结论：
①若用An－1 An表示第n条抛物线被x轴截得的线段的长，则A0A1=______， An－1 An=____________；
②是否存在经过点A1(b1,0)的直线和所有抛物线都相交，且被每一条抛物线截得的线段的长度都相等？若存在，直接写出直线的表达式；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
