
 如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75) 分析 根据楼高和山高可求出EF,继而得出AF,在Rt△AFC中表示出CF,在Rt△ABD中表示出BD,根据CF=BD可建立方程,解出即可.
解答 解:如图,过点C作CF⊥AB于点F.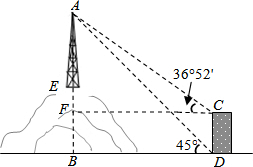
设塔高AE=x,作CF⊥AB于点F,
则四边形BDCF是矩形,
∴CD=BF=30m,CF=BD,
∵在Rt△ADB中,∠ADB=45°,
∴AB=BD=x+62,
∵在Rt△ACF中,∠ACF=36°52′,CF=BD=x+62,AF=x+62-30=x+32,
∴tan36°52′=$\frac{x+32}{x+62}$≈0.75,
∴x=58.
答:该铁塔的高AE为58米.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,注意利用方程思想求解,难度一般.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
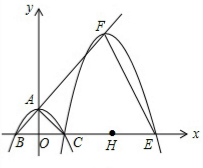 如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com