
问题背景:
在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中的一些物体进行了测量.下面是他们通过测量得到的一些信息:
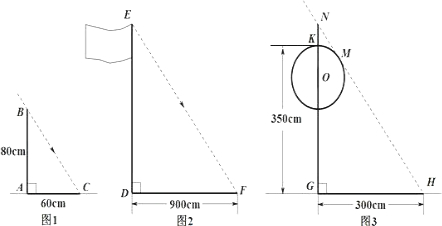
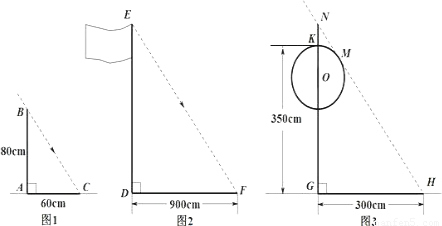
甲组:如图1,测得一根直立于平地,长为80 cm的竹竿的影长为60 cm.
乙组:如图2,测得学校旗杆的影长为900 cm.
丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)NG的影长为156 cm,KG=200 cm.

任务要求:
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图3,设太阳光线NH与圆O相切于点M,即OM⊥NH.请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:1562+2082=2602).
|
解:(1)由题意可知:∠BAC=∠EDF=90°,∠BCA=∠EFD. 所以△ABC∽△DEF. 所以 所以DE=1200(cm). 所以,学校旗杆的高度是12 m. (2)与(1)类似得: 所以GN=208 cm. 在Rt△NGH中,根据勾股定理得: NH2=1562+2082=2602. 所以NH=260 cm. 设圆O的半径为r cm, 因为OM⊥NH. 所以∠OMN=∠HGN=90°. 又∠ONM=∠HNG, 所以△OMN∽△HGN,所以 又ON=OK+KN=OK+(GN-GK)=r+8. 所以 所以,景灯灯罩的半径是12 cm. |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2009年江西省中考数学试题 题型:044
问题背景:在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:
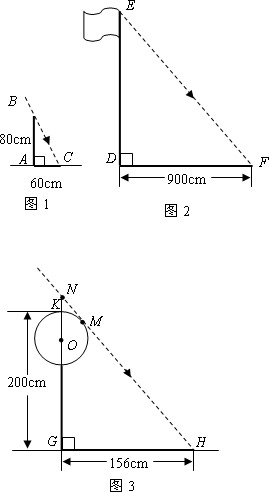
甲组:如图1,测得一根直立于平地,长为80 cm的竹竿的影长为60 cm.
乙组:如图2,测得学校旗杆的影长为900 cm.
丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200 cm,影长为156 cm.
任务要求
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年河北省张家口市中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com