已知等腰三角形的一腰上的中线把这个三角形的周长分为12和15两部分,求这个三角形的三边长.
分析:已知等腰三角形的一腰上的中线把这个三角形的周长分为12和15两部分,由于没有具体说明哪部分是12,哪部分是15;所以需分两种情况进行分析:第一种AB+AD=12,第二种AB+AD=15;由此可分别求得三角形的三边的长.
解答: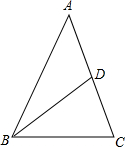
解:在△ABC中,AB=AC,BD是中线,设AB=x,BC=y
(1)当AB+AD=12时,则
解得∴三角形三边的长为8、8、11;
(2)当AB+AD=15时,则
解得∴三角形三边的长为10、10、7
经检验,两种情况均符合三角形三边关系定理
因此这个三角形的三边长分别为8,8,11或10,10,7.
点评:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

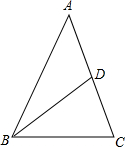 解:在△ABC中,AB=AC,BD是中线,设AB=x,BC=y
解:在△ABC中,AB=AC,BD是中线,设AB=x,BC=y
