
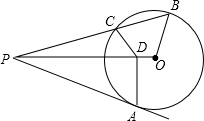
 如图,已知PA为⊙O的切线,割线PB交圆于B,C两点,连PO,AD⊥PO于D点,连接CD,BO,求证:∠PDC=∠PBO.
如图,已知PA为⊙O的切线,割线PB交圆于B,C两点,连PO,AD⊥PO于D点,连接CD,BO,求证:∠PDC=∠PBO. 分析 连结OA,如图,根据切线的性质得∠OAP=90°,则可判断△PDA∽△PAO,利用相似比可得PA2=PD•PO,再根据切割线定理得PA2=PC•PB,所以PD•PO=PC•PB,即$\frac{PC}{PO}$=$\frac{PD}{PB}$,加上∠DPC=∠BPO,则可判断△PCD∽△POB,然后根据相似三角形的性质即可得到结论.
解答 证明:连结OA,如图,
∵PA为⊙O的切线,
∴OA⊥AP,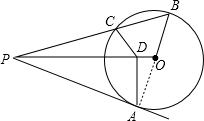
∴∠OAP=90°,
∵AD⊥OP,
∴∠PDA=90°,
而∠DPA=∠APO,
∴△PDA∽△PAO,
∴$\frac{PA}{PO}$=$\frac{PD}{PA}$,
∴PA2=PD•PO,
∵PA为切线,AB为割线,
∴PA2=PC•PB,
∴PD•PO=PC•PB,
即$\frac{PC}{PO}$=$\frac{PD}{PB}$,
而∠DPC=∠BPO,
∴△PCD∽△POB,
∴∠PDC=∠PBO.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
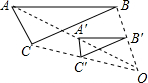 如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )
如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题:
张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
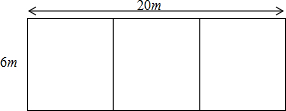 某农村为发展家庭养禽业,准备在墙外空坝上(墙长20米,空坝最窄处6米)利用现有的36米长的篱笆围成三个相连且面积相等的矩形鸡、鸭、鹅场各一个
某农村为发展家庭养禽业,准备在墙外空坝上(墙长20米,空坝最窄处6米)利用现有的36米长的篱笆围成三个相连且面积相等的矩形鸡、鸭、鹅场各一个查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com