
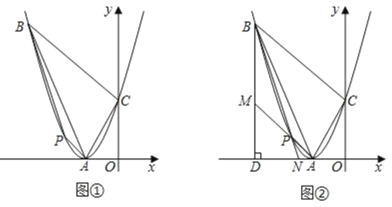
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为A(﹣2,0),且经过点B(﹣5,9),与y轴交于点C,连接AB,AC,BC.
(1)求该抛物线对应的函数表达式;
(2)点P为该抛物线上点A与点B之间的一动点.
①若S△PAB=![]() S△ABC,求点P的坐标.
S△ABC,求点P的坐标.
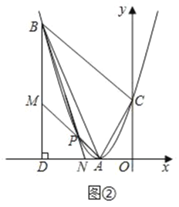
②如图②,过点B作x轴的垂线,垂足为D,连接AP并延长,交BD于点M.连接BP并延长,交AD于点N.试说明DN(DM+DB)为定值.
【答案】(1)y=x2+4x+4;(2)①P(﹣3,1)或(﹣4,4);②见解析,DN(DM+DB)为定值27.
【解析】
(1)利用顶点式设出抛物线解析式,再将点B坐标代入求解,即可得出结论;
(2)先求出直线BC解析式,进而求出三角形ABC的面积,得出三角形ABP的面积为3,设出点P坐标,表示出点G坐标,利用三角形ABP的面积为3建立方程求解即可得出结论;
②先设出直线BN的解析式y=k(x+5)+9①,得出DN,再设出直线AM的解析式为y=k'(x+2)②,进而得出DM,再联立①②求出点P坐标,再将点P坐标代入抛物线解析式中,得出k=k'3,即可得出结论.
解:(1)∵抛物线y=ax2+bx+c(a≠0)的顶点为A(﹣2,0),
∴设抛物线的解析式为y=a(x+2)2,
将点B(﹣5,9)代入y=a(x+2)2中,得,9=a(﹣5+2)2,
∴a=1,
∴抛物线的解析式为y=(x+2)2=x2+4x+4;
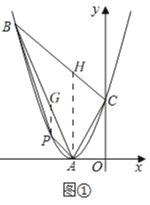
(2)①如图①,由(1)知,抛物线的解析式为y=x2+4x+4,
∴C(0,4),
∵B(﹣5,9),
∴直线BC的解析式为y=﹣x+4,
过点A作AH∥y轴,交直线BC于H,
过P作PG∥y轴,交直线BA于HG,
∵A(﹣2,0),
∴H(﹣2,6),
∴S△ABC=![]() AH×(xC﹣xB)=
AH×(xC﹣xB)=![]() ×6×5=15,
×6×5=15,
∵S△PAB=![]() S△ABC,
S△ABC,
∴S△PAB=![]() ×15=3,
×15=3,
∵A(﹣2,0),B(﹣5,9),
∴直线AB的解析式为y=﹣3x﹣6
设点P(p,p2+4p+4),
∴G(p,﹣3p﹣6),
∴S△PAB=![]() [﹣3p﹣6﹣(p2+4p+4)]×(﹣2+5)=3,
[﹣3p﹣6﹣(p2+4p+4)]×(﹣2+5)=3,
∴p=﹣3或p=﹣4,
∴P(﹣3,1)或(﹣4,4);
②如图②,
∵BD⊥x轴,且B(﹣5,9),
∴D(﹣5,0),
设直线BN的解析式为y=k(x+5)+9①,
令y=0,则k(x+5)+9=0,
∴x=﹣![]() =﹣5﹣
=﹣5﹣![]() ,
,
∴N![]() ,0),
,0),
∴DN=﹣5﹣![]() +5=﹣
+5=﹣![]() ,
,
∵点A(﹣2,0),
∴设直线AM的解析式为y=k'(x+2)②,
当x=5时,y=﹣3k',
∴M(﹣5,﹣3k'),
∴DM=﹣3k',
联立①②得![]() ,
,
解得, ,
,
∴P(﹣2﹣2×![]() ,﹣3k'×
,﹣3k'×![]() ),
),
∵点P在抛物线y=(x+2)2上,
∴(﹣2﹣3×![]() +2)2=﹣3k'×
+2)2=﹣3k'×![]() ,
,
∴![]() ,
,
∴k=k'﹣3,
∴DN(DM+DB)=﹣![]() (﹣3k'+9)=27×
(﹣3k'+9)=27×![]() (k'﹣3)=27×
(k'﹣3)=27×![]() ×k=27;
×k=27;
即:DN(DM+DB)为定值27.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②a+b+c≥ax2+bx+c;③若M(n2+1,y1),N(n2+2,y2)为函数图象上的两点,则y1>y2.④若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值2个.有其中正确的有( )个.
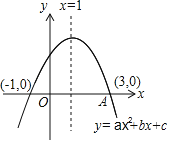
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丹要测量灯塔市葛西河生态公园里被湖水隔开的两个凉亭![]() 和
和![]() 之间的距离,她在
之间的距离,她在![]() 处测得凉亭
处测得凉亭![]() 在
在![]() 的南偏东
的南偏东![]() 方向,她从
方向,她从![]() 处出发向南偏东
处出发向南偏东![]() 方向走了
方向走了![]() 米到达
米到达![]() 处,测得凉亭
处,测得凉亭![]() 在
在![]() 的东北方向.
的东北方向.

(1)求![]() 的度数;
的度数;
(2)求两个凉亭![]() 和
和![]() 之间的距离(结果保留根号).
之间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如图的统计表和扇形图:

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 20 |
B | b | 18 |
C | c | 15 |
(1)①在扇形图中,a= ,C部门所对应的圆心角的度数为 .
②在统计表中,b= ,c= .
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的木条组成的几何图案,观察图形规律,解决下列问题:
 ……….
……….
(1)填空:第一个图案由1个正方形组成,共用的木条根数![]() ;
;
第二个图案由4个正方形组成,共用的木条根数![]() ;
;
第三个图案由9个正方形组成,共用的木条根数![]() ;
;
第四个图案由16个正方形组成,共用的木条根数![]() ;
;
(2)第![]() 个图案由
个图案由![]() 个正方形组成,共用木条根数
个正方形组成,共用木条根数![]() (用含
(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某实践小组为测量某大学的旗杆![]() 和教学楼
和教学楼![]() 的高,先在
的高,先在![]() 处用高
处用高![]() 米的测角仪测得旗杆顶端
米的测角仪测得旗杆顶端![]() 的仰角
的仰角![]() ,此时教学楼顶端
,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走
上,再向前走![]() 米到达
米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() ,点
,点![]() 三点在同一水平线上,(参考数据:
三点在同一水平线上,(参考数据:![]() )
)
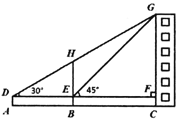
(1)计算旗杆![]() 的高;
的高;
(2)计算教学楼![]() 的高.
的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若抛物线![]() 顶点A的横坐标是
顶点A的横坐标是![]() ,且与y轴交于点
,且与y轴交于点![]() ,点P为抛物线上一点.
,点P为抛物线上一点.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 若将抛物线
若将抛物线![]() 向下平移4个单位,点P平移后的对应点为
向下平移4个单位,点P平移后的对应点为![]() 如果
如果![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
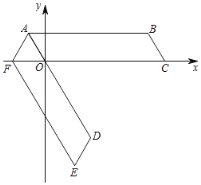
【题目】如图,四边形ABCO是平行四边形,OA=2,AB=8,点C在x轴的正半轴上,将平行四边形ABCO绕点A顺时针旋转得到平行四边形ADEF,AD恰好经过点O,点F恰好落在x轴的负半轴上.则点D的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com