
分析 分别过E、F、D三点作三边的平行线,依次计算△APE、△BFQ、△DRC与△ABC面积的比,最后利用求差法得出结论.
解答 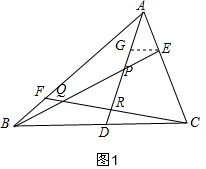 解:如图1,过E作EG∥BC交AD于G,
解:如图1,过E作EG∥BC交AD于G,
∵CE=2AE,
∴AC=3AE,
∴S△ABE=$\frac{1}{3}$S△ABC,
∵EG∥CD,
∴△AGE∽△ACD,
∴$\frac{EG}{DC}=\frac{AE}{AC}=\frac{1}{3}$,
∴CD=3EG,
同理△GEP∽△BDP,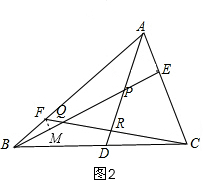
∴$\frac{PE}{BP}=\frac{GE}{BD}=\frac{EG}{CD}$=$\frac{1}{3}$,
∴BP=3PE,BE=4PE,
∴S△APE=$\frac{1}{4}$S△ABE=$\frac{1}{12}$S△ABC,
如图2,过F作FM∥AC,交BE于M,
∵AF=3BF,
∴AB=4BF,
∴S△BFC=$\frac{1}{4}$S△ABC,
∵FM∥AC,
∴△BFM∽△BAE,
∴$\frac{FM}{AE}=\frac{BF}{AB}$=$\frac{1}{4}$,
∴$\frac{FM}{EC}$=$\frac{1}{8}$,
同理得:△FMQ∽△CEQ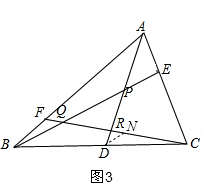 ,
,
∴$\frac{FQ}{CQ}=\frac{FM}{EC}$=$\frac{1}{8}$,
∴S△BFQ=$\frac{1}{9}$S△BFC=$\frac{1}{9}$×$\frac{1}{4}$S△ABC=$\frac{1}{36}$S△ABC,
如图3,过D作DN∥AB,交FC于N,
∵BD=DC,
∴FN=NC,
∴$\frac{DN}{BF}=\frac{1}{2}$,
∴S△ADC=$\frac{1}{2}$S△ABC,
∴$\frac{DN}{AF}$=$\frac{1}{6}$,
∵DN∥AF,
∴△DNR∽△AFR,
∴$\frac{DN}{AF}$=$\frac{DR}{AR}$=$\frac{1}{6}$,
∴S△DRC=$\frac{1}{7}$S△ADC=$\frac{1}{7}$×$\frac{1}{2}$S△ABC=$\frac{1}{14}$S△ABC,
∵S△BFC=S△BFQ+S四边形QBDR+S△DRC,
$\frac{1}{4}$S△ABC=$\frac{1}{36}$S△ABC+S四边形QBDR+$\frac{1}{14}$S△ABC,
∴S四边形QBDR=$\frac{19}{126}$S△ABC,
综上所述,∵S△ADC=S△APE+S四边形PDCE,
∴S四边形PDCE=$\frac{1}{2}{S}_{△ABC}$-$\frac{1}{12}{S}_{△ABC}$=$\frac{5}{12}{S}_{△ABC}$,
S△PQR=S△ABC-S△ABE-S四边形QBDR-S四边形PDCE,
=S△ABC-$\frac{1}{3}$S△ABC-$\frac{19}{126}$S△ABC-$\frac{5}{12}{S}_{△ABC}$,
=$\frac{25}{252}{S}_{△ABC}$.
答:S△PQR是三角形ABC面积的252分之25.
点评 本题是三角形的面积问题,考查了三角形的面积与底和高的关系,明确同高三角形面积的比等于对应底边的比,熟练掌握平行相似的判定方法,知道两三角形相似,对应边成比例.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -200元 | B. | 200元 | C. | 1200元 | D. | 2180元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?小颖解得此题的答案为48mm,小颖善于反思,她又提出如下的问题,如果,原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?小颖解得此题的答案为48mm,小颖善于反思,她又提出如下的问题,如果,原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com