
【题目】(10分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,然后求出BF=CE,再利用“边角边”证明△ABF和△DCE全等即可;
(2)根据全等三角形对应角相等可得∠BAF=∠EDC,然后求出∠DAF=∠EDA,然后根据等腰三角形的定义证明即可.
试题解析:(1)在矩形ABCD中,∠B=∠C=90°,AB=DC,
∵BE=CF,BF=BC-FC,CE=BC-BE,
∴BF=CE,
在△ABF和△DCE中,
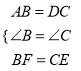 ,
,
∴△ABF≌△DCE(SAS);
(2)∵△ABF≌△DCE,
∴∠BAF=∠EDC,
∵∠DAF=90°-∠BAF,∠EDA=90°-∠EDC,
∴∠DAF=∠EDA,
∴△AOD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B,D作DE⊥a于点E,BF⊥a于点F,若DE=4,BF=3,则EF的长为( )
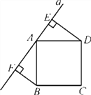
A. 1 B. 5 C. 7 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() ,
,![]() 在第一象限内的图象如图所示,点P1,P2,P3,…,P2018在反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,…,P2018在反比例函数![]() 图象上,它们的横坐标分别是
图象上,它们的横坐标分别是![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,纵坐标分别是1,3,5,…,共2018个连续奇数,过点P1,P2,P3,…,P2018分别作
,纵坐标分别是1,3,5,…,共2018个连续奇数,过点P1,P2,P3,…,P2018分别作![]() 轴的平行线,与
轴的平行线,与![]() 的图象交点依次是Q1(
的图象交点依次是Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,
,![]() ),Q3(
),Q3(![]() ,
,![]() ),…,Q2018(
),…,Q2018(![]() ,
,![]() ),则
),则![]() =_________.
=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0),D(﹣7,3),点B、C在第二象限内.
(1)求点B的坐标。
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD 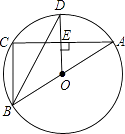
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com