
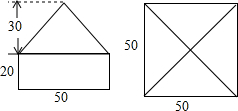
 如图是一个尖顶石柱的三视图(单位:厘米).如果每立方米的石料重2.4t,求这个尖顶石柱的质量.
如图是一个尖顶石柱的三视图(单位:厘米).如果每立方米的石料重2.4t,求这个尖顶石柱的质量. 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
| k1 |
| x |
| k2 |
| x |
| BC |
| AB |
| BC |
| AB |
| BC |
| AB |
| BC |
| AB |
| BC |
| AB |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
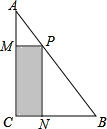 如图,将直角三角形余料截出一个矩形PMCN,∠C=90°,AC=40cm,BC=30cm,点P、M、N分别在AB、AC、BC上,设CN=x.
如图,将直角三角形余料截出一个矩形PMCN,∠C=90°,AC=40cm,BC=30cm,点P、M、N分别在AB、AC、BC上,设CN=x.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
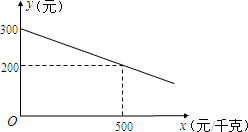 某公司生产一种环保产品,需要添加一种新型原料,若每件产品的利润与新型原料价格成一次函数关系,且每件产品的利润y(元)与新型原料的价格x(元/千克)的函数图象如图:
某公司生产一种环保产品,需要添加一种新型原料,若每件产品的利润与新型原料价格成一次函数关系,且每件产品的利润y(元)与新型原料的价格x(元/千克)的函数图象如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com