
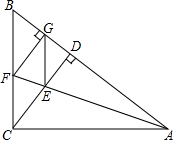
 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形. 分析 由角平分线的性质得出CF=GF,∠CAF=∠BAF,证出CD∥GF,由角的互余关系和对顶角相等得出∠CFE=∠AED=∠CEF,证出CE=CF,得出CE=GF,证出四边形CEGF是平行四边形,即可证出四边形CEGF是菱形.
解答 证明:∵AF平分∠BAC,∠ACB=90°,FG⊥AB于点G,
∴CF=GF,∠CAF=∠BAF,
∵CD⊥AB,
∴CD∥GF,
∵∠CFE+∠CAF=90°,∠AED+∠BAF=90°,
∴∠CFE=∠AED=∠CEF,
∴CE=CF,
∴CE=GF,
∴四边形CEGF是平行四边形,
又∵CE=CF,
∴四边形CEGF是菱形.
点评 本题考查了角平分线的定义、等腰三角形的判定与性质、平行四边形的判定、菱形的判定;本题有一定难度,证明三角形是等腰三角形是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
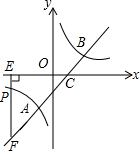 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
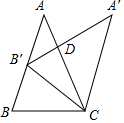 如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)
如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com