
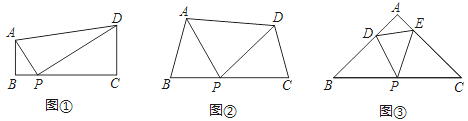
【题目】感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6![]() ,CE=4,则DE的长为 .
,CE=4,则DE的长为 .
【答案】感知:见解析;探究:证明见解析;拓展: ![]() .
.
【解析】
感知:先判断出,∠BAP=∠DPC,进而得出结论;
探究:同理根据两角相等相等,两三角形相似,进而得出结论;
拓展:利用相似三角形△BDP∽△CPE得出比例式求出BD,三角形内角和定理证得AC⊥AB且AC=AB;然后在直角△ABC中由勾股定理求得AC=AB=6;最后利用在直角△ADE中利用勾股定理来求DE的长度.
感知:∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠DPC,
∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
∴△ABP∽△DCP.
探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
拓展:同探究的方法得出,△BDP∽△CPE,
∴![]() ,
,
∵点P是边BC的中点,
∴BP=CP=3![]() ,
,
∵CE=4,
∴![]() ,
,
∴BD=![]() ,
,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,
即AC⊥AB且AC=AB=6,
∴AD=AB﹣BD=6﹣![]() =
=![]() ,AE=AC﹣CE=6﹣4=2,
,AE=AC﹣CE=6﹣4=2,
在Rt△ADE中,DE=![]() .
.
故答案是:![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
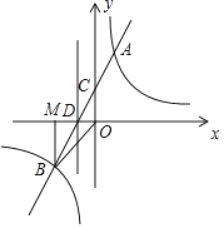
【题目】如图,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A,B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(k≠0)的图象交于第一、三象限内的A,B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(1)求该反比例函数和一次函数的表达式;
(2)直线AB交x轴于点D,过点D作直线l⊥x轴,如果直线l上存在点P,坐标平面内存在点Q.使四边形OPAQ是矩形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极配合我市文明城市创建,居委会组织了两个检查组,分别对辖区内新华园、清华园、德才园、御花园四个小区“垃圾分类”和“违规停车”的情况进行抽查,每个检查组随机抽取辖区内的一个小区进行检查.
(1)“违规停车”检查组抽到新华园小区的概率为_____;
(2)求两个组恰好同时抽到御花园小区进行检查的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为8,以AB为直径的圆交BC于点F.以C为圆心,CF长为半径作图,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 12
D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“校园朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
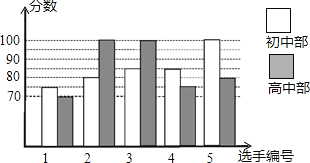
(1)根据图示填写表格;
平均分(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(2)结合两队成绩的平均数和中位数, 队的决赛成绩较好;
(3)已知高中代表队决赛成绩的方差为160,计算初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.(方差公式:S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]
)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
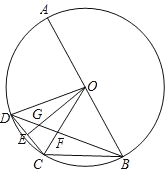
【题目】如图,AB是⊙O的直径,弦BC=OB,点D是![]() 上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
(1)求∠DGE的度数;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)记△CFB,△DGO的面积分别为S1,S2,若![]() =k,求
=k,求![]() 的值.(用含k的式子表示)
的值.(用含k的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com