
【题目】平面上有n条直线,其中没有两条直线互相平行(即每两条直线都相交),也没有三条或三条以上的直线通过同一点.试求:
(1)这n条直线共有多少个交点?
(2)这n条直线把平面分割为多少块区域?
【答案】
(1)
1条直线,0个交点
2条直线,1个交点
3条直线,1+2个交点
4条直线,1+2+3个交点
5条直线,1+2+3+4个交点
故n条直线,1+2+3+4+…+(n﹣1)个交点
∴n条直线,共有![]() 个交点;
个交点;
(2)
1条直线,将平面分成2个区域
2条直线,将平面分成2+2个区域
3条直线,将平面分成2+2+3个区域
4条直线,将平面分成2+2+3+4个区域
5条直线,将平面分成2+2+3+4+5个区域
故n条直线,将平面分成2+2+3+4+5+…+n个区域
∴n条直线,将平面分成![]() +1个区域.
+1个区域.
【解析】(1)1条直线,0个交点,2条直线,1个交点,3条直线,1+2个交点,4条直线,1+2+3个交点,故n条直线,1+2+3+4+…+(n﹣1)个交点;
(2)1条直线,将平面分成2个区域,2条直线,将平面分成2+2个区域,3条直线,将平面分成2+2+3个区域,4条直线,将平面分成2+2+3+4个区域,故n条直线,将平面分成2+2+3+4+5+…+n个区域.
【考点精析】利用平行公理对题目进行判断即可得到答案,需要熟知平行公理――平行线的存在性与惟一性;经过直线外一点,有且只有一条直线与这条直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
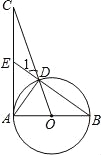
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.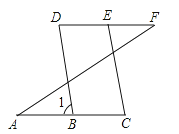
证明:∵∠A=∠F(已知)
∴AC∥ ,
∴∠D=∠1
又∵∠C=∠D(已知)
∴∠1=
∴BD∥CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.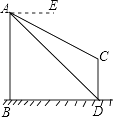
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=![]() ,b=
,b=![]() ,c=
,c=![]() ②a=6,∠A=45°; ③∠A=32°,∠B=58°;
②a=6,∠A=45°; ③∠A=32°,∠B=58°;
④a=7,b=24,c=25 ⑤a=2,b=2,c=4.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形,属于因式分解的是( )
A. (x+1)(x-1)=x2-1 B. m2+m-4=(m+3)(m-2)+2 C. x2+2x=x(x+2) D. x2-5x+6=x(x-5) +6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.
(1)试举一个例子来判断上述猜测结论是否成立
(2)若![]() 与
与![]() 互为相反数,求1﹣
互为相反数,求1﹣![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吉林省在践行社会主义核心价值观活动中,共评选出各级各类“吉林好人”45000多名,45000这个数用科学记数法表示为( )
A. 45×103 B. 4.5×104 C. 4.5×105 D. 0.45×103
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com