
【题目】如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.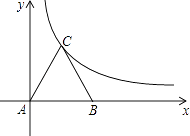
(1)求点C的坐标及反比例函数的解析式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.
【答案】
(1)解:过C点作CD⊥x轴,垂足为D
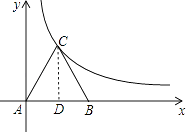
,设反比例函数的解析式为y= ![]() ,
,
∵△ABC是等边三角形,
∴AC=AB=6,∠CAB=60°,
∴AD=3,CD=sin60°×AC= ![]() ×6=3
×6=3 ![]() ,
,
∴点C坐标为(3,3 ![]() ),
),
∵反比例函数的图象经过点C,
∴k=9 ![]() ,
,
∴反比例函数的解析式y= ![]() ;
;
(2)解:若等边△ABC向上平移n个单位,使点B恰好落在双曲线上,
则此时B点的横坐标为6,
即纵坐标y= ![]() =
= ![]() ,也是向上平移n=
,也是向上平移n= ![]() .
.
【解析】(1)利用等边三角形的性质和三角函数的定义求出C坐标,利用待定系数法可求出反比例函数的解析式; (2)利用点向上平移时,坐标的变化规律,横同纵加,利用平移后横纵之积为![]() ,建立方程,求出n.
,建立方程,求出n.
【考点精析】解答此题的关键在于理解反比例函数的概念的相关知识,掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数.


科目:初中数学 来源: 题型:
【题目】∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).
(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB= °
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D
①若∠BAO=60°,则∠D= °.
②随着点A,B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由.
(3)如图③,延长MO至Q,延长BA至G,已知∠BAO,∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F,在△![]() 中,如果有一个角是另一个角的3倍,求∠ABO的度数.
中,如果有一个角是另一个角的3倍,求∠ABO的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PC=2PB.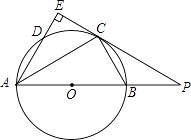
(1)探究线段PB,AB之间的数量关系,并说明理由;
(2)若AD=3,求AB长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中、∠BAD=120°,点O为射线CA 上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.
(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;
(2)如图②,点O在CA的延长线上,且OA=![]() AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;
AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;
(3)点O在线段AC上,若AB=6,BO=2![]() ,当CF=1时,请直接写出BE的长.
,当CF=1时,请直接写出BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
(1)求直线l2的解析式;
(2)求△BDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
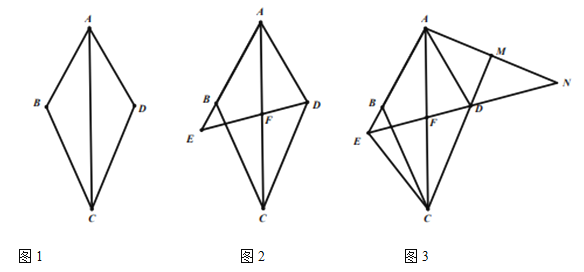
【题目】已知, 四边形![]() , 连接
, 连接![]() ,
,![]() ,
,![]() .
.
(1)如图![]() , 求证:
, 求证:![]() 平分
平分![]() ;
;
(2)如图![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在![]() 的条件下,连接
的条件下,连接![]() ,点
,点![]() 在
在![]() 延长线上,连接
延长线上,连接![]() ,延长
,延长![]() 与
与![]() 延长线交于点
延长线交于点![]() , 若
, 若![]() ,
,![]() ,
, ![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() ,
, ![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com