
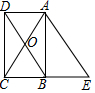
 如图,矩形ABCD的对角线AC与BD相交于点O,延长CB至点E,使BE=BC,连按AE.
如图,矩形ABCD的对角线AC与BD相交于点O,延长CB至点E,使BE=BC,连按AE.分析 (1)依据矩形的性质可知AD∥BE,AD=BC,结合条件BE=CB可得到AD=BE,然后依据一组对边平行且相等的四边形是平行四边形进行证明即可;
(2)依据矩形的性质可得到AC=BD=2OB=4,由ADBE为平行四边形可知AE=5,在Rt△ABE中,依据勾股定理可求得BE的长,最后依据平行四边形ADBE的周长=2×(BE+DE)求解即可.
解答 解:(1)∵ABCD为矩形,
∴AD=BC,AD∥BC.
又∵BC=BE,
∴BE=AD.
∵AD∥BE,
∴四边形ADBE为平行四边形.
(2)∵ABCD为矩形,OB=$\frac{5}{2}$,
∴AC=BD=5,∠ABE=90°
∵四边形ADBE为平行四边形,
∴AE=BD=5.
在Rt△ABE中,依据勾股定理可知:BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∴平行四边形ADBE的周长=2×(BE+DE)=2×(5+3)=16.
点评 本题主要考查的是矩形的性质、平行四边形的性质和判定、勾股定理的应用,熟练掌握相关知识是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1
在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
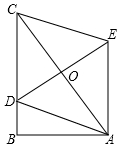 如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
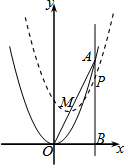 如图,直线x=2上有一点A(2,4),将抛物线y=x2的顶点在线段OA上移动到M,得到
如图,直线x=2上有一点A(2,4),将抛物线y=x2的顶点在线段OA上移动到M,得到查看答案和解析>>
科目:初中数学 来源: 题型:解答题
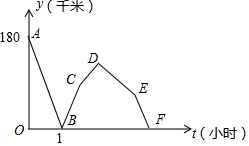 一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题:
一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com