
【题目】如图,在矩形![]() 中,点
中,点![]() 为对角线
为对角线![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
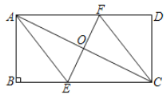
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析 (2)![]()
【解析】
(1)由矩形的性质可得∠ACB=∠DAC,然后利用“ASA”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,即可证四边形AECF是菱形;
(2)连接BD,![]() ,根据平行四边形的性质可得AF=CF=10,用勾股定理求得FD=6,在△BDC中,∠DCB=90°,用勾股定理求出BD的值,即可解答.
,根据平行四边形的性质可得AF=CF=10,用勾股定理求得FD=6,在△BDC中,∠DCB=90°,用勾股定理求出BD的值,即可解答.
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,

∴△AOF≌△COE(ASA),
∴OE=OF,且AO=CO,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(2)连接BD,![]()

![]() 四边形AFCE是平行四边形
四边形AFCE是平行四边形
![]() AF=CF=10
AF=CF=10
![]() ∠CDF=90°
∠CDF=90°
![]()
![]() CF=10,CD=AB=8
CF=10,CD=AB=8
![]() FD=6
FD=6
![]() AD=AF+DF=6+10=16
AD=AF+DF=6+10=16
![]() ∠DAB=90°
∠DAB=90°
![]() =
=![]() =
=![]()
![]() BO=
BO=![]()
故答案为:![]()


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 与点
与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,与边
,与边![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)![]() 与
与![]() 有什么样的数量关系?请直接写出你的结论:____________________
有什么样的数量关系?请直接写出你的结论:____________________
(2)![]() 、
、![]() 、
、![]() 的数量之间具有怎样的关系?并证明你所得到的结论.
的数量之间具有怎样的关系?并证明你所得到的结论.
(3)如果正方形的边长是1,![]() ,直接写出点
,直接写出点![]() 到直线
到直线![]() 的距离.
的距离.

解:(1)![]() 与
与![]() 的数量关系:____________________
的数量关系:____________________
(2)![]() 、
、![]() 、
、![]() 的数量之间的关系是 .
的数量之间的关系是 .
证明:
(3)点![]() 到直线
到直线![]() 的距离是 .
的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
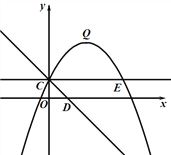
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊的毕达哥拉斯学派由古希腊哲学家毕达哥拉斯所创立,毕达哥拉斯学派认为数是万物的本原,事物的性质是由某种数量关系决定的,如他们研究各种多边形数:记第n个k边形数N(n,k)=![]() n2+
n2+![]() n(n≥1,k≥3,k、n都为整数),
n(n≥1,k≥3,k、n都为整数),
如第1个三角形数N(1,3)=![]() ×12+
×12+![]() ×1=1;
×1=1;
第2个三角形数N(2,3)=![]() ×22+
×22+![]() ×2=3;
×2=3;
第3个四边形数N(3,4)=![]() ×32+
×32+![]() ×3=9;
×3=9;
第4个四边形数N(4,4)=![]() ×42+
×42+![]() ×4=16.
×4=16.
(1)N(5,3)=________,N(6,5)=________;
(2)若N(m,6)比N(m+2,4)大10,求m的值;
(3)若记y=N(6,t)-N(t,5),试求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)
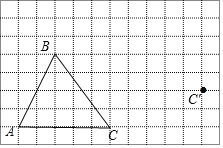
(1)画出平移后的△A′B′C′.
(2)画出AB边上的中线线CD;
(3)在整个平移过程中,线段BC扫过的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
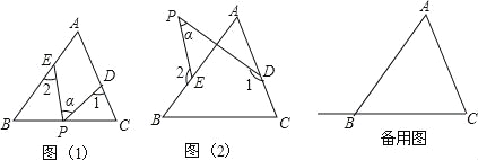
【题目】在△ABC中,∠A=50°,点D,E分别是边AC,AB上的点(不与A,B,C重合),点P是平面内一动点(P与D,E不在同一直线上),设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示,则∠1+∠2=________
(用α的代数式表示).
(2)若点P在ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边CB的延长线上运动时,试画出相应图形,标注有关字母与数字,并写出对应的∠α,∠1,∠2之间的关系式.(不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置。如图所示,
现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.
(1)画出△EDF;
(2)线段BD与AE有何关系? ____________;
(3)连接CD、BD,则四边形ABDC的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com