
分析 (1)①根据直角三角形的性质得到CD=$\frac{1}{2}$BC,根据全等三角形的性质得到BC=AE,等量代换得到CD=$\frac{1}{2}$AE,即可得到结论;②推出△ACB是等腰直角三角形,求得∠CBD=45°,证得B与E重合,根据等腰直角三角形的性质得到EF=$\frac{1}{2}$AE,根据矩形的性质得到EF=CD,即可得到结论;
(2)延长AC与直线L交于G,根据等腰三角形的性质得到BA=BG,证得CD∥AE,根据相似三角形的性质即可得到$\frac{CD}{AE}$的值;
(3)分情况讨论:①当点F在线段AB上时,过C作CG∥l交AE于H,交AB于G,推出△CFG∽△EFB,根据相似三角形的性质得到$\frac{CF}{EF}$=$\frac{5}{6}$,设CG=5x,BE=6x,则AB=10x,∵∠根据勾股定理得到AE=8x,由(2)得AE=2CD,根据相似三角形的性质得到$\frac{HG}{BE}$=$\frac{1}{2}$,于是得到CH=CG+HG=8,根据平行四边形的性质得到DE=CH=8,求得BD=DE=BE=2;②当点F在线段BA的延长线上时,过点C作CG∥l交AE于点H,交AB于G,同理可得求得结论.
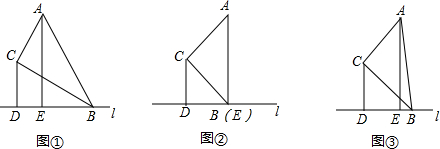
解答 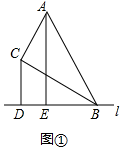 解:(1)①如图①,∵CD⊥BD,
解:(1)①如图①,∵CD⊥BD,
∴∠CDB=90°,
∵∠DBC=∠ABC=30°,
∴CD=$\frac{1}{2}$BC,
在△ABE与△ABC中,
$\left\{\begin{array}{l}{∠ACB=∠AEB=90°\\;}\\{∠BAE=∠ABC=30°}\\{AB=BA}\end{array}\right.$,
∴△ABC≌△ABE(AAS),
∴BC=AE,
∴CD=$\frac{1}{2}$AE,
∴$\frac{CD}{AE}$=$\frac{1}{2}$;
②如图②,∵∠ABC=45°,∠ACB=90°,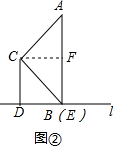
∴△ACB是等腰直角三角形,
∵∠CBD=45°,
∴∠ABD=90°,
∵AE⊥BC,
∴B与E重合,
∴EF=$\frac{1}{2}$AE,
∵CD⊥BD,
∴四边形CDEF的矩形,
∴EF=CD,
∴CD=$\frac{1}{2}$AE,
∴$\frac{CD}{AE}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$,$\frac{1}{2}$;
(2)$\frac{CD}{AE}$的值无变化,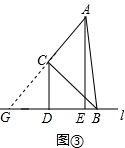
理由:如图③,延长AC与直线l交于G,
∴∠ABC=∠CBG,
∵∠ACB=90°,
∴∠AGB=∠BAG,
∴BA=BG,
又∵BC⊥AG,
∴C是AG的中点,
∵AE⊥l,CD⊥l,
∴CD∥AE,
∴△GCD∽△GAE,
∴$\frac{CD}{AE}$=$\frac{GC}{GA}$=$\frac{1}{2}$;
(3)分两种情况:
①如图④,当点F在线段AB上时,过C作CG∥l交AE于H,交AB于G,
∴∠DBC=∠HCB,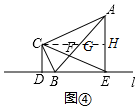
∵∠DBC=∠CBF,
∴∠CBF=∠HCB,
∴CG=BG,
∵∠ACB=90°,
∴∠CAG+∠CBF=∠HCB+∠ACG=90°,
∴∠ACG=∠CAG,
∴CG=AG=BG,
∵CG∥l,
∴△CFG∽△EFB,
∴$\frac{CF}{EF}$=$\frac{CG}{BE}$=$\frac{5}{6}$,
设CG=5x,BE=6x,则AB=10x,
∵∠AEB=90°,
∴AE=8x,
由(2)得AE=2CD,
∵CD=4,
∴AE=8=8x,
∴x=1,
∴AB=10,BE=6,CG=5,
∵GH∥l,
∴△AGH∽△ABE,
∴$\frac{HG}{BE}$=$\frac{AH}{AE}$=$\frac{1}{2}$,
∴HG=3,
∴CH=CG+HG=8,
∵CG∥l,CD∥AE,
∴四边形CDEH为平行四边形,
∴DE=CH=8,
∴BD=DE-BE=2;
②如图⑤,当点F在线段BA的延长线上时,
过点C作CG∥l,交AE于点H,交AB于G,
同理可得CG=5,BE=6,HG=3,
∴DE=CH=CG-HG=2,
∴BD=DE+BE=8,
综上所述,线段BD的长为2或8.
点评 本题属于相似形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,矩形、平行四边形的判定和性质,等腰直角三角形的性质以及勾股定理的综合应用,正确的作出辅助线,构造相似三角形和矩形是解题的关键.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
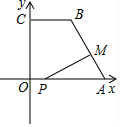 如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
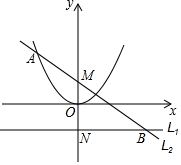 已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值.
已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
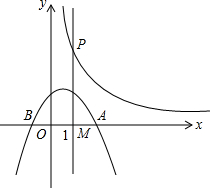 如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.
如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com