
【题目】九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一样),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
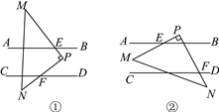
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读以下内容:
已知实数x,y满足x+y=2,且![]() 求k的值.
求k的值.
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于x,y的方程组![]() ,再求k的值.
,再求k的值.
乙同学:先将方程组中的两个方程相加,再求k的值.
丙同学:先解方程组![]() ,再求k的值.
,再求k的值.
(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题,再对你选择的思路进行简要评价.
(评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等)
请先在以下相应方框内打勾,再解答相应题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求点A、B、C的坐标;
(2)当点M和点N都在线段AC上时,连接EN,如果点E的坐标为(4,0),求sin∠ANE的值;
(3)在刻度尺平移过程中,当以点P、Q、N、M为顶点的四边形是平行四边形时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以![]() ,解得
,解得![]() ,
,
所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
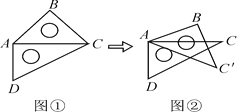
【题目】取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转得到△ABC′,如图②所示.设∠CAC′=α(0°<α≤45°).
(1)当α=15°时,求证:AB∥CD;
(2)连接BD,当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC的度数是否变化,若变化 ,求出变化范围;若不变,求出其度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,
轴上,![]() 轴,
轴,![]() 轴.点
轴.点![]() 从点
从点![]() 出发,以1个单位长度/秒的速度,沿五边形
出发,以1个单位长度/秒的速度,沿五边形![]() 的边顺时针匀速运动一周,若顺次连接
的边顺时针匀速运动一周,若顺次连接![]() ,
,![]() ,
,![]() 三点所围成的三角形的面积为
三点所围成的三角形的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() 秒,已知
秒,已知![]() 与
与![]() 之间的函数关系如图②中折线
之间的函数关系如图②中折线![]() 所示.
所示.
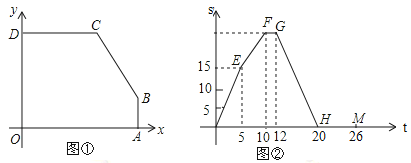
(1)图①中点![]() 的坐标为 ;点
的坐标为 ;点![]() 的坐标为 ;
的坐标为 ;
(2)求图②中![]() 所在直线的解析式;
所在直线的解析式;
(3)是否存在点![]() ,使
,使![]() 的面积为五边形
的面积为五边形![]() 的面积的
的面积的![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
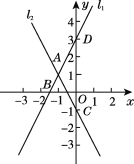
【题目】已知直线l1:y1=2x+3与直线l2:y2=kx-1交于点A,点A的横坐标为-1,且直线l1与x轴交于点B,与y轴交于点D,直线l2与y轴交于点C.
(1)直线l2对应的函数表达式;
(2)连接BC,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣ ![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为 .
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为 . 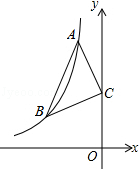
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com