
如图,已知二次函数y=﹣x2+bx+c的图象经过A(﹣2,﹣1),B(0,7)两点.
(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,y>0?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.

解:(1)————3分
∵二次函数y=﹣x2+bx+c的图象经过A(﹣2,﹣1),B(0,7)两点.
∴ ,
,
解得: ,
,
∴y=﹣x2+2x+7,
=﹣(x2﹣2x)+7,
=﹣[(x2﹣2x+1)﹣1]+7,
=﹣(x﹣1)2+8,
∴对称轴为:x=1.
(2)————3分
当y=0时,
0=﹣(x﹣1)2+8,
∴x﹣1=±2 ,
,
x1=1+2 ,x2=1﹣2
,x2=1﹣2 ,
,
∴抛物线与x轴交点坐标为:(1﹣2 ,0),(1+2
,0),(1+2 ,0),
,0),
∴当1﹣2 <x<1+2
<x<1+2 时,y>0;
时,y>0;
(3)————4分
当矩形CDEF为正方形时,
假设C点坐标为(x,﹣x2+2x+7),
∴D点坐标为(﹣x2+2x+7+x,﹣x2+2x+7),
即:(﹣x2+3x+7,﹣x2+2x+7),
∵对称轴为:x=1.
∴﹣x2+3x+7﹣1=﹣x+1,
解得:x1=﹣1,x2=5,
x=﹣1时,﹣x2+2x+7=4.
∴C点坐标为:(﹣1,4).


科目:初中数学 来源: 题型:
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:BE=BF;
(2)若∠CAE=30°,求∠ACF度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题是真命题的是( )
A.对角线相等且互相垂直的四边形是菱形 B.平移不改变图形的形状和大小
C.对角线互相垂直的梯形是等腰梯形 D.相等的弦所对的弧相等
查看答案和解析>>
科目:初中数学 来源: 题型:
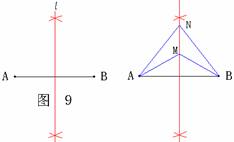
如图9,已知线段AB.
(1)用尺规作图的方法作出线段AB 的垂直平分线l (保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方).连结AM、AN、BM、BN.求证:∠MAN=∠MBN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com