练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．已知?ABCD中，∠B=46°，则∠D的度数为（　　）
    A．44°B．46°C．72°D．144°

    分析 由平行四边形的对角相等即可得出答案．

    解答 解：∵四边形ABCD是平行四边形，
    ∴∠D=∠B=46°，
    故选：B．

    点评 本题考查了平行四边形的性质；熟记平行四边形的对角相等是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．已知：如图，△ABC中，∠ACB=90°，D为AB边中点，点F在BC边上，DE∥CF，且DE=CF．若DF=2，EB的长为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．请仅用无刻度的直尺，作出下列各图中∠AOB的平分线，保留作图痕迹．
    （1）如图1中，OA=OB，BD=AC；
    （2）如图2中的每个小方格都是边长为1的正方形，A、O、B都在格点上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

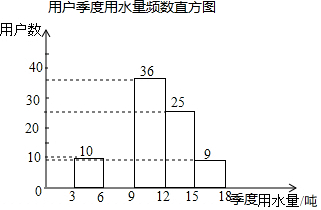    20．某社区为了进一步提高居民珍惜谁、保护水和水忧患意识，提倡节约用水，从本社区5000户家庭中随机抽取100户，调查他们家庭每季度的平均用水量，并将调查的结果绘制成如下的两幅不完整的统计图和表：
    用户季度用水量频数分布表
    平均用水量（吨）频数频率
    3＜x≤6100.1
    6＜x≤9m0.2
    9＜x≤12360.36
    12＜x≤1525n
    15＜x≤1890.09
    请根据上面的统计图表，解答下列问题：
    （1）在频数分布表中：m=20，n=0.25；
    （2）根据题中数据补全频数直方图；
    （3）如果自来水公司将基本季度水量定为每户每季度9吨，不超过基本季度用水量的部分享受基本价格，超出基本季度用水量的部分实行加价收费，那么该社区用户中约有多少户家庭能够全部享受基本价格？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

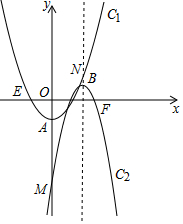    7．如图，抛物线C1：y1=tx2-1（t＞0）和抛物线C2：y2=-4（x-h）2+1（h≥1）．
    （1）两抛物线的顶点A、B的坐标分别为（0，1）和（h，1）；
    （2）设抛物线C2的对称轴与抛物线C1交于点N，则t为何值时，A、B、M、N为顶点的四边形是平行四边形．
    （3）设抛物线C1与x轴的左交点为点E，抛物线C2与x轴的右边交点为点F，试问，在第（2）问的前提下，四边形AEBF能否为矩形？若能，求出h值；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

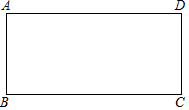    17．如图，在四边形ABCD中，已知AB∥DC，AB=DC，在不添加任何辅助线的情况下，请补充一个条件，使四边形ABCD成为矩形，这个条件是∠A=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知：如图，∠2=2∠1，∠3=3∠2，求∠DOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．数据0.0056用科学记数法表示为5.6×10-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列性质中，矩形具有但平行四边形不一定具有的是（　　）
    A．对边相等B．对角相等C．对角线相等D．对角线互相平分

    查看答案和解析>>

    同步练习册答案