
����Ŀ�����Ķ����в��ϣ�
���⣺��ͼ����������![]() ��ƽ���ı���
��ƽ���ı���![]() �У���
����![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��
̽������![]() ��
��![]() �ļн�Ϊ���ٶ�ʱ��ƽ���ı���
�ļн�Ϊ���ٶ�ʱ��ƽ���ı���![]() �������Σ�
��������
С��ͬѧ��˼·�ǣ����ȿ���˵���ı���![]() �Ǿ��Σ�Ȼ���ӳ�
�Ǿ��Σ�Ȼ���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������ȫ�������Σ�������������̽��������Ĵ𰸣�
������ȫ�������Σ�������������̽��������Ĵ𰸣�
����ο�С��ͬѧ��˼·��̽�������������⣮
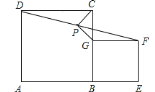
��1����֤���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��2��![]() ��
��![]() �ļн�Ϊ________��ʱ���ı���
�ļн�Ϊ________��ʱ���ı���![]() �������Σ�
��������
���ɣ�
���𰸡�(1)�����������2��90.
��������
��1����������ABCD���á�EBG��90����������һ������ֱ�ǵ�ƽ���ı����Ǿ��Σ�����֤���ı���BEFG�Ǿ��Σ�
��2�������������ߣ��ӳ�GP��DC�ڵ�H��������������ƽ���ı��ε����ʣ�����AAS����DHP�ա�FGP������HP��GP������CPG��90��ʱ������SAS��֤��CPH�ա�CPG������ȫ���������������ε����ʣ����ɵ�BG��GF��������һ���ڱ���ȵ�ƽ���ı��������Σ��ɵ�BEFG�����Σ�����EBG��90���������ı���BEFG�������Σ�
��1����������ABCD�У���ABC��90�㣬
���EBG��90�㣬
��BEFG�Ǿ�����
��2��90�㣻
���ɣ��ӳ�GP��DC�ڵ�H��
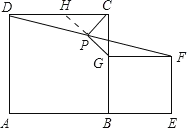
��������ABCD��ƽ���ı���BEFG�У�AB��DC��BE��GF��
��DC��GF��
���HDP����GFP����DHP����FGP��
��P���߶�DF���е㣬
��DP��FP��
���DHP�ա�FGP��
��HP��GP��
����CPG��90��ʱ����CPH����CPG��
��CP��CP��
���CPH�ա�CPG��
��CH��CG��
��������ABCD��DC��BC��
��DH��BG��
�ߡ�DHP�ա�FGP��
��DH��GF��
��BG��GF��
��BEFG������
�ɣ�1��֪�ı���BEFG�Ǿ��Σ�
���ı���BEFG�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �ǹ���
�ǹ���![]() �Ķ��κ�������
�Ķ��κ�������
![]() ����������
����������![]() ֵ��
ֵ��
![]() Ϊ��ֵʱ������������͵㣿��������͵㣮��ʱ����
Ϊ��ֵʱ������������͵㣿��������͵㣮��ʱ����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() �����������
�����������
![]() Ϊ��ֵʱ�����������ֵ�����ֵ�Ƕ��٣���ʱ����
Ϊ��ֵʱ�����������ֵ�����ֵ�Ƕ��٣���ʱ����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() �����������
�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����˵���ı���![]() �����ε��У� ��
�����ε��У� ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ��
��

A. �� B. ���� C. �� D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ���ҽ��ܼ��ŵĺ��٣����������Լ�õ磬���д�2016��7��1���𣬾����õ�ʵ����һ��һ�����������ݵ�����������������շѣ���һ�����õ���������180ǧ��ʱʵ����������������ڶ�������ʵ������ߵ�����������շ����������ͼ�������ͼ��ش��������⣺
(1)���õ�����180ǧ��ʱʱ�������___Ԫ��
(2)�������������___Ԫ/ǧ��ʱ��
(3)С����12�·ݵĵ����328.5Ԫ������������õ����ǧ��ʱ?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У���
����![]() �DZ�
�DZ�![]() �ϵĵ㣨��
�ϵĵ㣨��![]() ��
��![]() ���㲻�غϣ�������
���㲻�غϣ�������![]() ��
��![]() ��
��![]() ���ֱ�
���ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ���㣬����˵����ȷ���ǣ� ��
���㣬����˵����ȷ���ǣ� ��

A. ��![]() �����ı���
�����ı���![]() �Ǿ���
�Ǿ���
B. ��![]() ��ֱƽ��
��ֱƽ��![]() �����ı���
�����ı���![]() �Ǿ���
�Ǿ���
C. ��![]() �����ı���
�����ı���![]() ������
������
D. ��![]() ƽ��
ƽ��![]() �����ı���
�����ı���![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���״����С��ȫ��ͬ�ij�����ֽƬΧ�����Σ���ͼ������4��������ֽƬΧ�ɵ������Σ�����Ӱ���ֵ����Ϊ16����ͼ������8��������ֽƬΧ�ɵ������Σ�����Ӱ���ֵ����Ϊ8����ͼ������12��������ֽƬΧ�ɵ������Σ�������Ӱ���ֵ��ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() �ϵĵ㣬����
�ϵĵ㣬����![]() ��ʹ�ı���
��ʹ�ı���![]() Ϊ�����Σ�����
����������![]() ��
��![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ����������
����������![]() �۵�ʹ�õ�
�۵�ʹ�õ�![]() ����������
����������![]() �ĶԽ������ڵ�ֱ���ϣ���Ӧ��Ϊ
�ĶԽ������ڵ�ֱ���ϣ���Ӧ��Ϊ![]() �����߶�
�����߶�![]() �ij�Ϊ________��
�ij�Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y��kx+b��ͼ��x���ڵ�A����2��0������y���ڵ�B��������������Χ�ɵ������ε����Ϊ8����ú����ı���ʽΪ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com