Question

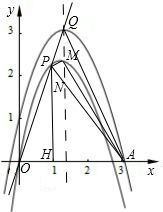
如图，已知在直角坐标平面内，点A的坐标为（3，0），第一象限内的点P在直线y=2x上，∠PAO=45度．
（1）求点P的坐标；
（2）如果二次函数的图象经过P、O、A三点，求这个二次函数的解析式，并写出它的图象的顶点坐标M；
（3）如果将第（2）小题中的二次函数的图象向上或向下平移，使它的顶点落在直线y=2x上的点Q处，求△APM与△APQ的面积之比．

Answer 1

分析：（1）根据题意设点P的坐标为（x，2x），又由∠PAO=45°，PH⊥OA，可得PH=AH=2x，又由点A的坐标为（3，0），即可求得x的值，则可求得点P的坐标；
（2）利用待定系数法将点P，O，A的坐标代入解析式即可得到方程组，解方程组即可求得解析式；
（3）根据图形求得：△APO、△AQO与四边形AMPO的面积，即可求得△APM与△APQ的面积，则问题得解．

解答：解：（1）过点P作PH⊥OA，垂足为点H．
∵点P在直线y=2x上，
∴设点P的坐标为（x，2x）．
∵∠PAO=45°，PH⊥OA，
∴∠PAO=∠APH=45°．
∴PH=AH=2x．
∵点A的坐标为（3，0），
∴x+2x=3．
∴x=1．
∴点P的坐标为（1，2）．

（2）设所求的二次函数解析式为y=ax²+bx+c（a≠0）．
∵图象经过P（1，2）、O（0，0）、A（3，0）三点，
∴

2=a+b+c  0=c  0=9a+3b+c

，
解得

a=-1  b=3  c=0

，
∴所求的二次函数解析式为y=-x²+3x．
顶点M的坐标为（

3

2

，

9

4

）．

（3）根据题意，得点Q的坐标为（

3

2

，3）．
∵S_△AQO=

1

2

×3×3=

9

2

，
S_△APO=

1

2

×3×2=3，
S_{四边形AMPO}=

1

2

×1×2+

1

2

×（2+

9

4

）×

1

2

+

1

2

×

3

2

×

9

4

=

15

4

，
∴S_△APM=

15

4

-3=

3

4

，S_△APQ=

9

2

-3=

3

2

．
∴△APM与△APQ的面积之比为

1

2

．
另解：根据题意，得点Q的坐标为（

3

2

，3）．
设图象的对称轴与直线AP相交于点N，则点N的坐标为（

3

2

，

3

2

）．
∴MN=

9

4

-

3

2

=

3

4

，QN=3-

3

2

=

3

2

．
∴MN=

1

2

QN，
∴

S△PMN

S△PQN

=

1

2

，

S△AMN

S△AQN

=

1

2

．
∴△APM与△APQ的面积之比为

1

2

．

点评：本题主要考查了二次函数解析式的确定、函数图象交点的求法以及三角形面积的求法等知识点．主要考查学生数形结合的数学思想方法．