
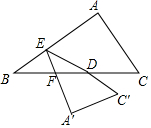
 在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.
在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$. 分析 根据∠B为锐角,分两种情况进行讨论:当∠BEF=90°时,△BEF为直角三角形;当∠BFE=90°时,△BEF为直角三角形,分别根据等腰直角三角形的性质,三角形中位线定理,轴对称的性质以及直角三角形的边角关系进行计算,即可得到BE的长度.
解答 解:分两种情况:
①如图,当∠BEF=90°时,△BEF为直角三角形,
过D作DM⊥AB于M,则∠EMD=90°,DM∥AC,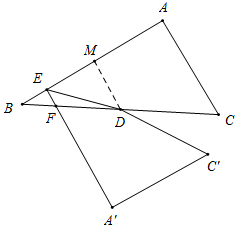
∵D为BC的中点,
∴M为AB的中点,
∴BM=$\frac{1}{2}$AB=2,DM=$\frac{1}{2}$AC=$\frac{3}{2}$,
由折叠可得,∠MED=$\frac{1}{2}$∠AEF=45°,
∴△DEM是等腰直角三角形,
∴EM=DM=$\frac{3}{2}$,
∴BE=2-$\frac{3}{2}$=$\frac{1}{2}$;
②如图,当∠BFE=90°时,△BEF为直角三角形,
连接AD,A'D,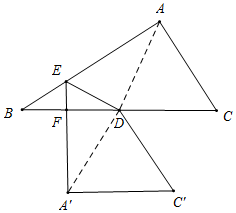
根据对称性可得,∠EAD=∠DA'D,AD=A'D
∵Rt△ABC中,AC=3,AB=4,
∴BC=5,
∵Rt△ABC中,D为BC的中点,
∴AD=BD=A'D=$\frac{1}{2}$BC=$\frac{5}{2}$,
∴∠B=∠EAD,
∴∠B=∠FA'D,
设BE=x,则BF=BE×cosB=$\frac{4}{5}$x,
∴DF=BD-BF=$\frac{5}{2}$-$\frac{4}{5}$x,
又∵Rt△A'DF中,sin∠FA'D=sinB,即$\frac{DF}{A'D}$=$\frac{3}{5}$
∴$\frac{\frac{5}{2}-\frac{4}{5}x}{\frac{5}{2}}=\frac{3}{5}$,
解得x=$\frac{5}{4}$,
即BE=$\frac{5}{4}$,
综上所述,BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.
点评 本题主要考查了折叠问题,直角三角形的性质,三角形中位线定理,轴对称的性质以及解直角三角形的运用,解决问题的关键是依据△BEF为直角三角形,画出图形进行分类讨论.


科目:初中数学 来源: 题型:选择题
| A. | a=$\sqrt{1}$,b=$\sqrt{2}$,c=$\sqrt{3}$ | B. | a=2,b=3,c=4 | C. | a=12,b=5,c=13 | D. | a=$\sqrt{7}$,b=2,c=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\frac{x}{7}$=$\frac{y}{3}$,则$\frac{x+y}{x-y}$=$\frac{5}{2}$ | B. | 若2x-5y=0,则$\frac{x-2y}{y}$=$\frac{1}{2}$ | ||
| C. | 若线段a:b=c:d,则$\frac{a+b}{c+d}=\frac{b}{d}$ | D. | 若线段a:b=c:d,则$\frac{a+m}{b+m}$=$\frac{c}{d}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
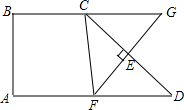 如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=BC,∠D=45°,CD的垂直平分线交CD于E,交AD于F,交BC的延长线于G,若AD=a.
如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=BC,∠D=45°,CD的垂直平分线交CD于E,交AD于F,交BC的延长线于G,若AD=a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
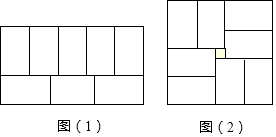 小明做拼图游戏时发现:8个完全相同的小长方形恰好可以拼成一个大长方形,如图(1)所示,小丽看见后,也想试一试,结果拼成了如图(2)所示的正方形,不过中间有一处空白,空白处恰好是边长为2cm的小正方形,请求出每个小长方形的长和宽.
小明做拼图游戏时发现:8个完全相同的小长方形恰好可以拼成一个大长方形,如图(1)所示,小丽看见后,也想试一试,结果拼成了如图(2)所示的正方形,不过中间有一处空白,空白处恰好是边长为2cm的小正方形,请求出每个小长方形的长和宽.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 小明 | 小华 | 小芳 | |
| 笔记本(本) | 15 | 24 | 27 |
| 钢笔(支) | 25 | 40 | 45 |
| 总价(元) | 330 | 528 | 585 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com