
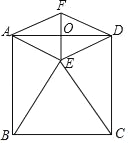
【题目】如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.
(1)请直接写出∠AEB的度数,∠AEB= ;
(2)将△AED沿直线AD向上翻折,得△AFD.求证:四边形AEDF是菱形;
(3)连接EF,交AD于点 O,试求EF的长?
【答案】(1)75°;(2)证明见解析;(3)![]()
【解析】
试题(1)由正方形和等边三角形的性质得出∠ABE=30°,AB=BE,由等腰三角形的性质和三角形内角和定理即可求出∠AEB的度数;
(2)先判断出△ABE≌△DCE,得到AE=ED,再由翻折的性质即可得出结论;
(3)先由等边三角形的性质求出EH,进而得出OE,借助(2)的结论即可求出EF.
试题解析:(1)∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∵△EBC是等边三角形,
∴BE=BC,∠EBC=60°,
∴∠ABE=90°-60°=30°,AB=BE,
∴∠AEB=∠BAE=![]() (180°-30°)=75°;
(180°-30°)=75°;
(2)∵四边形ABCD为正方形,
∴∠ABC=∠BCD=90°,AB=CD,
∵△BCE为等边三角形,
∴∠BCE=∠EBC=60°,BE=EC,
∴∠ABE=∠DCE=90°-60°=30°,
∴△ABE≌△DCE,
∴AE=ED,
∵△AED沿着AD翻折为△AFD,
∴AE=ED=AF=FD,
∴四边形AEDF是菱形;
(3)如图,
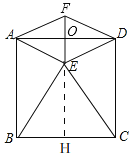
由翻折知,AE=AF,∠FAO=∠EAO,
∴EF⊥AD,过点E作EH⊥BC于H,
在等边三角形BCE中,BC=2,
∴EH=![]() BC=
BC=![]() ,
,
∴EO=OH-EH=AB-EH=2-![]() ,
,
∴EF=2EO=2(2-![]() )=4-2
)=4-2![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
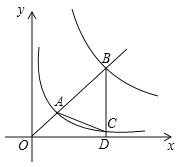
【题目】(2017浙江省湖州市,第16题,4分)如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数![]() 和
和![]() 在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交
在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交![]() 的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
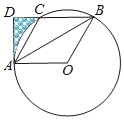
【题目】如图,⊙O的半径为6,点A,B,C为⊙O上三点,BA平分∠OBC,过点A作AD⊥BC交BC延长线于点D.
(1)求证:AD是⊙O的切线;
(2)当sin∠OBC=![]() 时,求BC的长;
时,求BC的长;
(3)连结AC,当AC∥OB时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:
(1)若小明随机选择一个插座插入,则插入A的概率为 ;
(2)现小明对手机和学习机两种电器充电,请用列表或画树状图的方法表示出两个插头插入插座的所有可能情况,并计算两个插头插在相邻插座的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
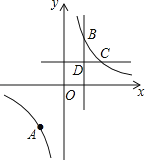
【题目】已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.
(1)当y1﹣y2=4时,求m的值;
(2)如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
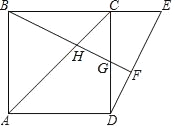
【题目】如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:GDAB=DFBG;
(2)联结CF,求证:∠CFB=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com