
【题目】提出问题:
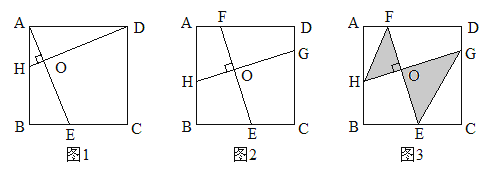
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在边AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积。
【答案】(1)证明见解析(2)EF=GH(3)![]()
【解析】(1)由正方形的性质可得AB=DA,∠ABE=90°=∠DAH.又由∠ADO+∠OAD=90°,可证得∠HAO=∠ADO,继而证得△ABE≌△DAH,可得AE=DH;
(2)将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.根据(1)的结论得AM=DN,所以EF=GH;
(3)过点F作FP⊥BC于点P,易证得△AHF∽△CGE,即可求得EC,AF的长,继而求得EF的长,然后由平行线分线段成比例定理,求得![]() ,然后分别求出△FOH与△EOG的面积,即可求得答案.
,然后分别求出△FOH与△EOG的面积,即可求得答案.
(1)证明:∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAH,
∴∠HAO+∠OAD=90°,
∵AE⊥DH,
∴∠ADO+∠OAD=90°,
∴∠HAO=∠ADO,
∴△ABE≌△DAH(ASA),
∴AE=DH;
(2)EF=GH,理由如下:
将FE平移到AM处,则AM∥EF,AM=EF,
将GH平移到DN处,则DN∥GH,DN=GH,

∵EF⊥GH,
∴AM⊥DN,
根据(1)的结论得AM=DN,所以EF=GH;
(3)解:∵四边形ABCD是正方形,
∴AB∥CD,
∴∠AHO=∠CGO,
∵FH∥EG,
∴∠FHO=∠EGO,
∴∠AHF=∠CGE,
∴△AHF∽△CGE,
∴![]() ,
,
∵EC=2,
∴AF=1,
过F作FP⊥BC于点P,
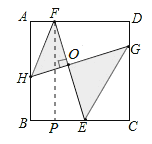
根据勾股定理得EF=![]() ,
,
∵FH∥EG,
∴![]() ,
,
根据(2)知EF=GH,
∴FO=HO,
∴![]() ,
,
![]() ,
,
∴阴影部分面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)己知:如图,△ABC,∠C=90°,现将斜边AB绕A点顺时针旋转90°到AD,过D点作DE⊥CA,交CA的延长线于点E.求证:△ABC ≌ △DAE
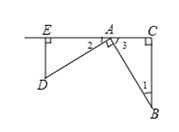
(2)如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的高BD,CE相交于点O.请你添加一个条件,使BD=CE.你所添加的条件是________.(仅添加一对相等的线段或一对相等的角)
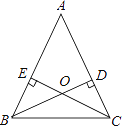
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为![]() 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人![]() 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过![]() 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:
(1)如果去乙草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(2)如果![]() 个人去甲草莓园采摘
个人去甲草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(3)小颖和妈妈准备采摘![]() 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
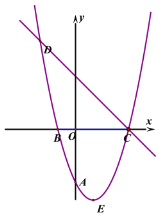
【题目】已知抛物线![]() 经过A(0,-3),B(-1,0),且抛物线对称轴为直线
经过A(0,-3),B(-1,0),且抛物线对称轴为直线![]() ,E
,E
是抛物线的顶点。
(1)求抛物线的解析式以及顶点坐标E。
(2)在![]() 轴上是否存在点P,使得
轴上是否存在点P,使得![]() 周长最短,若存在,请求出P点坐标,若不存在,请说
周长最短,若存在,请求出P点坐标,若不存在,请说
明理由。
(3)直线![]() 与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
使得![]() 的面积最大,若存在请求出最大面积,若不存在,请说明理由。
的面积最大,若存在请求出最大面积,若不存在,请说明理由。
(4)抛物线上是否存在点M,使得![]() 是直角三角形,若存在,直接写出M点坐标,若不
是直角三角形,若存在,直接写出M点坐标,若不
存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过![]() km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方![]() m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为![]() m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个三角形中,一定全等的是()
A. 两个等边三角形
B. 有一个角是![]() ,腰相等的两个等腰三角形
,腰相等的两个等腰三角形
C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是![]() ,底相等的两个等腰三角形
,底相等的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )

A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
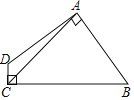
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com