
【题目】如图,在平面直角坐标系中,已知某个二次函数的图象经过点A(1,2),B(2,﹣1),C(4,﹣1),且该二次函数的最小值是﹣2.
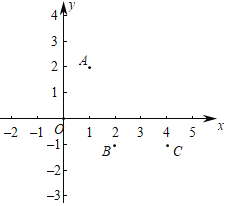
(1)请在图中描出该函数图象上另外的两个点,并画出图象;
(2)求出该二次函数的解析.
【答案】(1)见解析;(2)y=x2﹣6x+7.
【解析】
(1)根据B、C两点的坐标和函数最小值,可以确定函数的对称轴以及函数的顶点坐标,然后根据抛物线的对称性,找到对称点,连线即可.
(2)已知抛物线的对称轴和顶点坐标,所以设顶点式,然后找到一个点(非顶点坐标)代入求解计算即可.
(1)∵B(2,﹣1),C(4,﹣1),且该二次函数的最小值是﹣2.
∴该二次函数图象的顶点为(3,﹣2),
∵点A(1,2),
∴A关于对称轴对称的点为(5,2),
利用描点法可画出函数图象,如图;

(2)设抛物线的解析式为y=a(x﹣3)2﹣2,
代入A(1,2)得2=4a﹣2,解得a=1,
∴该二次函数的解析式为y=x2﹣6x+7.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:抛物线y=2ax2﹣ax﹣3(a+1)与x轴交于点AB(点A在点B的左侧).
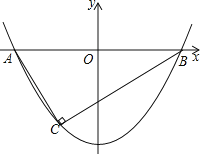
(1)不论a取何值,抛物线总经过第三象限内的一个定点C,请直接写出点C的坐标;
(2)如图,当AC⊥BC时,求a的值和AB的长;
(3)在(2)的条件下,若点P为抛物线在第四象限内的一个动点,点P的横坐标为h,过点P作PH⊥x轴于点H,交BC于点D,作PE∥AC交BC于点E,设△ADE的面积为S,请求出S与h的函数关系式,并求出S取得最大值时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)在给定的直角坐标系中,画出这个函数的图象;

(2)根据图象,写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)若将此图象沿![]() 轴向左平移3个单位,向下移动2个单位,请写出平移后图象所对应的函数表达式.
轴向左平移3个单位,向下移动2个单位,请写出平移后图象所对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在线段AB上,AO=4,OB=2,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做运动,设运动时间为t秒.

(1)当t=1秒时,则OP= ,S△ABP= ;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.为了求AQBP的值,小华同学尝试过O点作OE∥AP交BP于点E,试利用小华同学给我们的启发补全图形并求AQBP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
![]()
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①②B. ①③C. ①②③D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com