
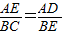 ;
;
 ,
,
 ,
,
 ,
,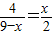 ,
,

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
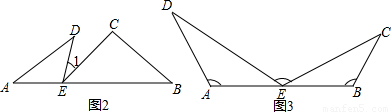
 (1)尝试:如图,已知A、E、B三点在同一直线上,且∠A=∠B=∠DEC=90°,
(1)尝试:如图,已知A、E、B三点在同一直线上,且∠A=∠B=∠DEC=90°,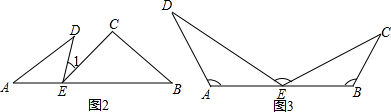
 重合),连接AP,过点P作PE交CD于点E,使得∠APE=∠ABC.则当BP为何值时,点E为CD的中点.
重合),连接AP,过点P作PE交CD于点E,使得∠APE=∠ABC.则当BP为何值时,点E为CD的中点.查看答案和解析>>
科目:初中数学 来源:风华金帆同步训练·数学·七年级下册(新课标人教版) 新课标人教版 题型:044
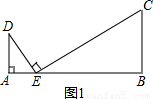
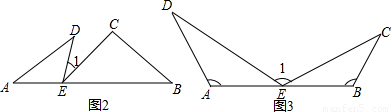
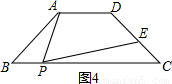
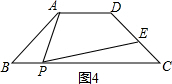
如图,已知AB∥CD,分别猜想出下列四个图形中∠A,∠C,∠P的关系,并尝试说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:044
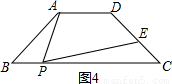
如图,要测量河两岸相对的两点A,B间的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得的DE的长就是AB的长,你能根据测量的过程把已知的条件和未知的条件用数学语言叙述出来吗?请尝试着说一说.
小颖是这样叙述的:如图,已知AB⊥BD,ED⊥BD,垂足分别为B,D,点C在BD上,且BC=CD,点A,C,E在一条直线上,则ED=AB.
请你说说这是为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)尝试:如图,已知A、E、B三点在同一直线上,且∠A=∠B=∠DEC=90°,
(1)尝试:如图,已知A、E、B三点在同一直线上,且∠A=∠B=∠DEC=90°,
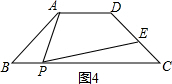 重合),连接AP,过点P作PE交CD于点E,使得∠APE=∠ABC.则当BP为何值时,点E为CD的中点.
重合),连接AP,过点P作PE交CD于点E,使得∠APE=∠ABC.则当BP为何值时,点E为CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com