
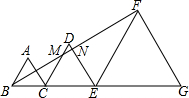
 如图,△ABC、△DCE、△FEG为等边三角形,边长分别为2、3、5,且从左至右如图排列,连接BF,交DC、DE分别于M、N两点,则△DMN的面积为$\frac{\sqrt{3}}{8}$.
如图,△ABC、△DCE、△FEG为等边三角形,边长分别为2、3、5,且从左至右如图排列,连接BF,交DC、DE分别于M、N两点,则△DMN的面积为$\frac{\sqrt{3}}{8}$. 分析 易证BE=EF=5,从而可得∠EBF=$\frac{1}{2}$∠FEG=30°,根据三角形外角的性质可得到∠DNM=90°;易证△BCM∽△BEF,根据相似三角形的性质可求出CM,从而得到DM的值,然后在Rt△DNM中,运用三角函数可求出MN、DN,就可求出△DMN的面积.
解答 解:∵△FEG为等边三角形,∴∠FEG=60°.
∵BC=2,CE=3,EF=5,∴BE=5=EF,
∴∠EBF=∠EFB=$\frac{1}{2}$∠FEG=30°.
∵△DCE为等边三角形,
∴∠D=∠DCE=∠DEC=60°,
∴∠DNM=∠EBF+∠DEC=90°.
∵∠DCE=∠FEG=60°,
∴CM∥EF,
∴△BCM∽△BEF,
∴$\frac{CM}{EF}$=$\frac{BC}{BE}$,即$\frac{CM}{5}$=$\frac{2}{5}$,
解得CM=2,
∴DM=DC-CM=3-2=1,
∴在Rt△DNM中,
MN=DM•sin60°=$\frac{\sqrt{3}}{2}$,
DN=DM•cos60°=$\frac{1}{2}$,
∴S△DNM=$\frac{1}{2}$DN•MN=$\frac{\sqrt{3}}{8}$.
故答案为$\frac{\sqrt{3}}{8}$.
点评 本题主要考查了相似三角形的判定与性质、等边三角形的性质、等腰三角形的性质、三角形外角的性质、三角函数的定义等知识,本题除了运用三角形相似求CM的值,还可以通过证明∠CBM=∠CMB=30°,得到CM=BC=2.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
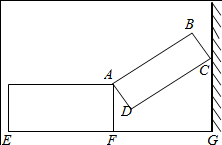 如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.
如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
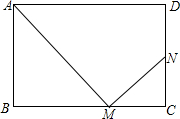 在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
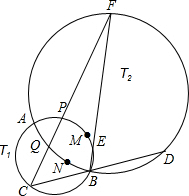 如图,两圆T1、T2相交于A、B两点,过点B的一条直线分别交圆T1、T2于点C、D,过点B的另一条直线分别交圆T1、T2于点E、F,直线CF分别交圆T1、T2于点P、Q,设M、N分别是弧PB、弧QB的中点,求证:若CD=EF,则C、F、M、N四点共圆.
如图,两圆T1、T2相交于A、B两点,过点B的一条直线分别交圆T1、T2于点C、D,过点B的另一条直线分别交圆T1、T2于点E、F,直线CF分别交圆T1、T2于点P、Q,设M、N分别是弧PB、弧QB的中点,求证:若CD=EF,则C、F、M、N四点共圆.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com