

 解:过点A作AD⊥BC,垂足为D.
解:过点A作AD⊥BC,垂足为D. ≈
≈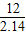 ≈5.61.
≈5.61.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
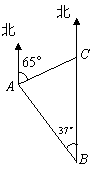
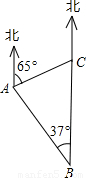
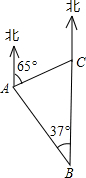 如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障,已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离.(结果精确到0.1海里)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14.)
如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障,已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离.(结果精确到0.1海里)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14.)查看答案和解析>>
科目:初中数学 来源: 题型:
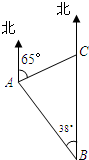 如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西38°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离(结果精确到1海里).
如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西38°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离(结果精确到1海里).查看答案和解析>>
科目:初中数学 来源: 题型:
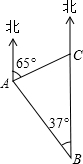 如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求BC之间的距离(结果精确到0.1海里).
如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求BC之间的距离(结果精确到0.1海里).查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一巡逻艇航行至海面![]() 处时,得知其正北方向上
处时,得知其正北方向上![]() 处一渔船发生故障.已知港口
处一渔船发生故障.已知港口![]() 处在
处在![]() 处的北偏西
处的北偏西![]() 方向上,距
方向上,距![]() 处20海里;
处20海里;![]() 处在A处的北偏东
处在A处的北偏东![]() 方向上.
方向上.
求![]() 之间的距离(结果精确到0.1海里).
之间的距离(结果精确到0.1海里).
参考数据:![]()
![]()
 |
查看答案和解析>>
科目:初中数学 来源:2009-2010学年山东省泰安市九年级(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com