
分析 将$\frac{3{x}^{2}+6x+5}{\frac{1}{2}{x}^{2}+x+1}$变形为6-$\frac{1}{\frac{1}{2}{x}^{2}+x+1}$,$\frac{{x}^{2}+2x-2}{{x}^{2}+2x+2}$变形为1$-\frac{4}{{x}^{2}+2x+2}$,然后求得分母的最大值从而可求得答案.
解答 解:$\frac{3{x}^{2}+6x+5}{\frac{1}{2}{x}^{2}+x+1}$=$\frac{3{x}^{2}+6x+6-1}{\frac{1}{2}{x}^{2}+x+1}$=6-$\frac{1}{\frac{1}{2}{x}^{2}+x+1}$,
当x=-$\frac{b}{2a}$=-1时,$\frac{1}{2}{x}^{2}+x+1$有最大值,最大值为$\frac{1}{2}$.
∴6-$\frac{1}{\frac{1}{2}}$=6-2=4.
∴分式$\frac{3{x}^{2}+6x+5}{\frac{1}{2}{x}^{2}+x+1}$的最小值是4.
$\frac{{x}^{2}+2x-2}{{x}^{2}+2x+2}$=$\frac{{x}^{2}+2x+2-4}{{x}^{2}+2x+2}$=1$-\frac{4}{{x}^{2}+2x+2}$,
当x=-1时,x2+2x+2有最小值,最小值为1.
∴1-$\frac{4}{1}$=-3.
∴分式$\frac{{x}^{2}+2x-2}{{x}^{2}+2x+2}$的最小值为-3.
故答案为:4;-3.
点评 本题主要考查的是二次函数的最值,能够将分式进行正确变形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 45° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.5~7.5 | B. | 7.5~9.5 | C. | 9.5~11.5 | D. | 11.5~13.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
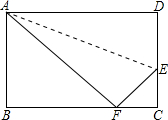 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com