
 如图,四边形ABCO方形,△BEF是等腰直角三角形,∠EBF=90°,点C,E在x轴上,点A在y轴上,点F在双曲线y=$\frac{k}{x}$(k≠0)第一象限内的图象上,S△BEF=5,OC=1,则k=8.
如图,四边形ABCO方形,△BEF是等腰直角三角形,∠EBF=90°,点C,E在x轴上,点A在y轴上,点F在双曲线y=$\frac{k}{x}$(k≠0)第一象限内的图象上,S△BEF=5,OC=1,则k=8. 分析 过点F作FG⊥y轴于点G,延长CB交FG于点H,设点F(x,$\frac{k}{x}$),证△BHF≌△ECB得HF=BC=1,EC=BH=$\frac{k}{x}$-1,由HF=x-1得x-1=1,即x=2,根据S△BEF=$\frac{1}{2}$BE2=5得BE=BF=$\sqrt{10}$,根据EC2+BC2=BE2得($\frac{k}{x}$-1)2+1=10,即($\frac{k}{2}$-1)2+1=10,解之可得答案.
解答 解:过点F作FG⊥y轴于点G,延长CB交FG于点H,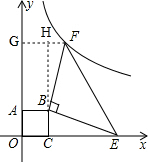
∵四边形ABCO是正方形,且OC=1,
∴BH⊥FG,
∴∠BHF=∠ECB=90°,
∴∠HBF+∠HFB=90°,
又∵∠EBF=90°,且BE=BF,
∴∠HBF+∠EBC=90°,
∴∠HFB=∠EBC,
在△BHF和△ECB中,
∵$\left\{\begin{array}{l}{∠BHF=∠ECB}\\{∠HFB=∠CBE}\\{BF=EB}\end{array}\right.$,
∴△BHF≌△ECB,
设点F(x,$\frac{k}{x}$)
∴HF=BC=1,EC=BH=$\frac{k}{x}$-1,
∵HF=x-1,
则x-1=1,即x=2,
又∵S△BEF=$\frac{1}{2}$BE2=5,
∴BE=BF=$\sqrt{10}$,
∵EC2+BC2=BE2,
∴($\frac{k}{x}$-1)2+1=10,即($\frac{k}{2}$-1)2+1=10,
解得:k=8或k=-4<0(舍),
故答案为:8.
点评 本题主要考查全等三角形的判定与性质、正方形的性质、等腰三角形的性质等知识点,熟练掌握全等三角形的判定与性质及根据勾股定理得出关于k的方程是解题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
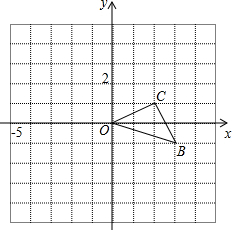 如图,已知O是坐标原点,以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),则B(3,-1)的对称点的坐标为(-6,2).
如图,已知O是坐标原点,以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),则B(3,-1)的对称点的坐标为(-6,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
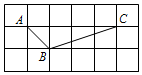 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
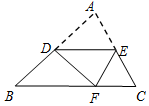 如图,D是AB的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上点F处,若∠B=50°,则∠EDF的度数为( )
如图,D是AB的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上点F处,若∠B=50°,则∠EDF的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
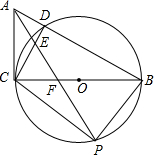 如图,在△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交AB于点D,连接CD,∠CAB的角平分线交CD于点E,交BC于点F,交⊙O于点P.
如图,在△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交AB于点D,连接CD,∠CAB的角平分线交CD于点E,交BC于点F,交⊙O于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
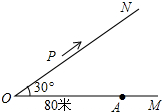 如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.
如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com