
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃН2x2+4x+kЉ1ЃЎ
ЃЈ1ЃЉЕБЖўДЮКЏЪ§ЕФЭМЯѓгыxжсгаНЛЕуЪБЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєAЃЈx1ЃЌ0ЃЉгыBЃЈx2ЃЌ0ЃЉЪЧЖўДЮКЏЪ§ЭМЯѓЩЯЕФСНИіЕуЃЌЧвЕБxЃНx1+x2ЪБЃЌyЃНЉ6ЃЌЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЌВЂдкЫљЬсЙЉЕФзјБъЯЕжаЛГіДѓжТЭМЯѓЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋХзЮяЯпдкxжсЯТЗНЕФВПЗжбиxжсЗелЃЌЭМЯѓЦфгрВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓЃЌЕБжБЯпyЃН![]() x+mЃЈmЃМ3ЃЉгыаТЭМЯѓгаСНИіЙЋЙВЕуЃЌЧвmЮЊећЪ§ЪБЃЌЧѓmЕФжЕЃЎ
x+mЃЈmЃМ3ЃЉгыаТЭМЯѓгаСНИіЙЋЙВЕуЃЌЧвmЮЊећЪ§ЪБЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉkЁм3ЃЛЃЈ2ЃЉyЃН2x2+4xЉ6ЃЌКЏЪ§ЭМЯѓМћНтЮіЃЛЃЈ3ЃЉmЃН1Лђ0ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнИљЕФХаБ№ЪНЁї=b2-4acКЭНЛЕуЕФИіЪ§ПЩжБНгЧѓНтЃЛ
ЃЈ2ЃЉИљОнЬтвтЧѓГіКЏЪ§ОЙ§ЕФЕуЃЈ-2ЃЌ-6ЃЉЃЌШЛКѓДњШыКЏЪ§ЕФНтЮіЪНМДПЩЧѓГіkЕФжЕЃЌДгЖјЕУЕНКЏЪ§ЕФНтЮіЪНЃЌЛГіЭМЯёЃЛ
ЃЈ3ЃЉИљОнЬтвтЛГіЗелКѓЕФЭМаЮЃЌИљОнЭМаЮЧѓГіСНИіНЛЕуЪБЕФЭМЯёЮЛжУЃЌЧѓГіmЕФМДПЩ.
ЃЈ1ЃЉИљОнЬтвтжЊb2Љ4acЃН16Љ8ЃЈkЉ1ЃЉЁн0ЃЌ
НтЕУЃКkЁм3ЃЛ
ЃЈ2ЃЉгЩЬтвтжЊ![]() ЃЌ
ЃЌ
Ёрx1+x2ЃНЉ2ЃЌ
ЁрХзЮяЯпЙ§ЕуЃЈЉ2ЃЌЉ6ЃЉЃЌ
НЋЃЈЉ2ЃЌЉ6ЃЉДњШыyЃН2x2+4x+kЉ1ЃЌЕУЃК8Љ8+kЉ1ЃНЉ6ЃЌ
НтЕУЃКkЃНЉ5ЃЌ
дђХзЮяЯпНтЮіЪНЮЊyЃН2x2+4xЉ6ЃЌ
ЦфКЏЪ§ЭМЯѓШчЯТЃК
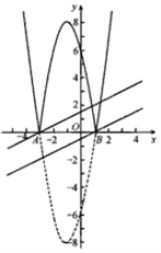
ЃЈ3ЃЉШчЭМЫљЪОЃЌЁпmЃМ3ЃЌ
ЁрЕБжБЯпЙ§ЃЈ1ЃЌ0ЃЉЪБЃЌжБЯпyЃН![]() x+mгыаТЭМЯѓга1ИіНЛЕуЃЌ
x+mгыаТЭМЯѓга1ИіНЛЕуЃЌ
ДЫЪБ![]() +mЃН0ЃЌМДmЃН-
+mЃН0ЃЌМДmЃН-![]() ЃЛ
ЃЛ
ЕБжБЯпЙ§ЃЈ-3ЃЌ0ЃЉЪБЃЌжБЯпyЃН![]() x+mгыаТЭМЯѓга3ИіНЛЕуЃЌ
x+mгыаТЭМЯѓга3ИіНЛЕуЃЌ
ДЫЪБ![]() +mЃН0ЃЌМДmЃН
+mЃН0ЃЌМДmЃН![]() ЃЛ
ЃЛ
НсКЯЭМаЮжЊЉ![]() ЃМmЃМ
ЃМmЃМ![]() ЃЌ
ЃЌ
ЁпmЮЊећЪ§ЃЌ
ЁрmЃН1Лђ0ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
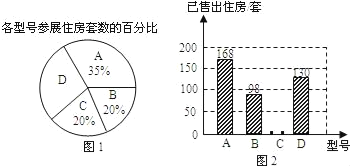
ЁОЬтФПЁПдкЁА2010ФъжиЧьДКМОЗПНЛЛсЁБЦкМфЃЌФГЗПЕиВњПЊЗЂЦѓвЕЭЦГіAЁЂBЁЂCЁЂDЫФжжРраЭЕФзЁЗПЙВ1000ЬзНјааеЙЯњЃЌCаЭКХзЁЗПЯњЪлЕФГЩНЛТЪЮЊ50%ЃЌЦфЫќаЭКХзЁЗПЕФЯњЪлЧщПіЛцжЦдкЭМ1КЭЭМ2СНЗљЩаВЛЭъећЕФЭГМЦЭМжаЃЎ
(1)ВЮМгеЙЯњЕФDаЭКХзЁЗПЬзЪ§ЮЊЁЁ ЁЁЬзЃЎ
(2)ЧыФуНЋЭМ2ЕФЭГМЦЭМВЙГфЭъећЃЎ
(3)ШєгЩ2ЬзAаЭКХзЁЗП(гУA1ЃЌA2БэЪО)ЃЌ1ЬзBаЭКХзЁЗП(гУBБэЪО)ЃЌ1ЬзCаЭКХзЁЗП(гУCБэЪО)зщГЩЬиМлЗПдДЃЌВЂДгжаГщГі2ЬззЁЗПЃЌНЋетСНЬззЁЗПЕФШЋВПЯњЪлПюОшИјЧрКЃгёЪїЕие№джЧјЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓГі2ЬззЁЗПОљЪЧAаЭКХЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌBCЃН2ABЃЌEЃЌFЗжБ№ЪЧBCЃЌADЕФжаЕуЃЌAEЃЌBFНЛгкЕуOЃЌСЌНгEFЃЌOCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABEFЪЧСтаЮЃЛЃЈ2ЃЉШєBCЃН8ЃЌЁЯABCЃН60ЁуЃЌЧѓOCЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌЭМЯѓЙ§ЕуЃЈ-1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпx=2ЃЌЯТСаНсТлЃКЃЈ1ЃЉ4a+b=0ЃЛЃЈ2ЃЉ9a+cЃО3bЃЛЃЈ3ЃЉ8a+7b+2cЃО0ЃЛЃЈ4ЃЉШєЕуAЃЈ-3ЃЌy1ЃЉЁЂЕуBЃЈ-![]() ЃЌy2ЃЉЁЂЕуCЃЈ
ЃЌy2ЃЉЁЂЕуCЃЈ![]() ЃЌy3ЃЉдкИУКЏЪ§ЭМЯѓЩЯЃЌдђy1ЃМy3ЃМy2ЃЛЃЈ5ЃЉШєЗНГЬaЃЈx+1ЃЉЃЈx-5ЃЉ=-3ЕФСНИљЮЊx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђx1ЃМ-1ЃМ5ЃМx2ЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
ЃЌy3ЃЉдкИУКЏЪ§ЭМЯѓЩЯЃЌдђy1ЃМy3ЃМy2ЃЛЃЈ5ЃЉШєЗНГЬaЃЈx+1ЃЉЃЈx-5ЃЉ=-3ЕФСНИљЮЊx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђx1ЃМ-1ЃМ5ЃМx2ЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ

A. 2ИіB. 3ИіC. 4ИіD. 5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+3ЕФЭМЯѓЗжБ№гыxжсНЛгкЕуAЃЈ3ЃЌ0ЃЉЃЌCЃЈ-1ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЎЕуDЮЊЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуЃЎ
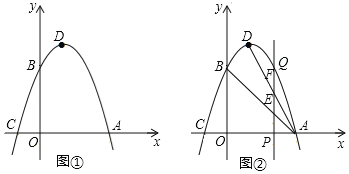
ЃЈ1ЃЉШчЭМЂйЫљЪОЃЌЧѓДЫЖўДЮКЏЪ§ЕФЙиЯЕЪНЃК
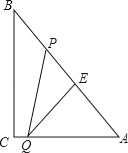
ЃЈ2ЃЉШчЭМЂкЫљЪОЃЌдкxжсЩЯШЁвЛЖЏЕуPЃЈmЃЌ0ЃЉЃЌЧв1ЃМmЃМ3ЃЌЙ§ЕуPзїxжсЕФДЙЯпЗжБ№НЛЖўДЮКЏЪ§ЭМЯѓЁЂЯпЖЮADЃЌABгкЕуQЁЂFЃЌEЃЌЧѓжЄЃКEF=EPЃЛ
ЃЈ3ЃЉдкЭМЂйжаЃЌШєRЮЊyжсЩЯЕФвЛИіЖЏЕуЃЌСЌНгARЃЌдђ![]() BR+ARЕФзюаЁжЕ______ЃЈжБНгаДГіНсЙћЃЉЃЎ
BR+ARЕФзюаЁжЕ______ЃЈжБНгаДГіНсЙћЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌBCЃН8cmЃЌACЃН6cmЃЎЕуPДгBГіЗЂбиBAЯђAдЫЖЏЃЌЫйЖШЮЊУПУы1cmЃЌЕуEЪЧЕуBвдPЮЊЖдГЦжааФЕФЖдГЦЕуЃЌЕуPдЫЖЏЕФЭЌЪБЃЌЕуQДгAГіЗЂбиACЯђCдЫЖЏЃЌЫйЖШЮЊУПУы2cmЃЌЕБЕуQЕНДяЖЅЕуCЪБЃЌPЃЌQЭЌЪБЭЃжЙдЫЖЏЃЌЩшPЃЌQСНЕудЫЖЏЪБМфЮЊtУыЃЎ
(1)ЕБtЮЊКЮжЕЪБЃЌPQЁЮBCЃП
(2)ЩшЫФБпаЮPQCBЕФУцЛ§ЮЊyЃЌЧѓyЙигкtЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЫФБпаЮPQCBУцЛ§ФмЗёЪЧЁїABCУцЛ§ЕФ![]() ЃПШєФмЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЃПШєФмЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
(4)ЕБtЮЊКЮжЕЪБЃЌЁїAEQЮЊЕШбќШ§НЧаЮЃПЃЈжБНгаДГіНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊв§ЕМбЇЩњЙуЗКдФЖСЮФбЇУћжјЃЌФГаЃдкЦпФъМЖЁЂАЫФъМЖПЊеЙСЫЖСЪщжЊЪЖОКШќ. ИУаЃЦпЁЂАЫФъМЖИїгабЇЩњ400ШЫЃЌ ИїЫцЛњГщШЁ20УћбЇЩњНјааСЫГщбљЕїВщЃЌЛёЕУСЫЫћУЧжЊЪЖОКШќГЩМЈЃЈЗжЃЉЃЌВЂЖдЪ§ОнНјааећРэЁЂУшЪіКЭЗжЮі. ЯТУцИјГіСЫВПЗжаХЯЂ.
ЦпФъМЖЃК74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
АЫФъМЖЃК76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
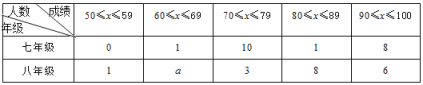
ЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчЯТБэЫљЪОЃК

ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
(1)a= ЃЌm= ЃЌn= ЃЛ
(2)ФуШЯЮЊФФИіФъМЖЖСЪщжЊЪЖОКШќЕФзмЬхГЩМЈНЯКУЃЌЫЕУїРэгЩЃЈжСЩйДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦЖЯЕФКЯРэадЃЉЃЛ
(3)ИУаЃЖдЖСЪщжЊЪЖОКШќГЩМЈВЛЩйгк80ЗжЕФбЇЩњЪкгшЁАдФЖСаЁФмЪжЁБГЦКХЃЌЧыФуЙРМЦИУаЃЦпЁЂАЫФъМЖЫљгабЇЩњжаЛёЕУЁАдФЖСаЁФмЪжЁБГЦКХЕФДѓдМга ШЫ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌвбжЊ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() БпЩЯвЛЕуЃЈВЛгы
БпЩЯвЛЕуЃЈВЛгы![]() жиКЯЃЉЃЌвд
жиКЯЃЉЃЌвд![]() ЮЊжБОЖзї
ЮЊжБОЖзї![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() Ча
Ча![]() гк
гк![]() ЃЌНЛ
ЃЌНЛ![]() гк
гк![]() .
.
ЃЈ1ЃЉШє![]() ЕФАыОЖЮЊ2ЃЌЧѓЯпЖЮ
ЕФАыОЖЮЊ2ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФАыОЖЃЛ
ЕФАыОЖЃЛ
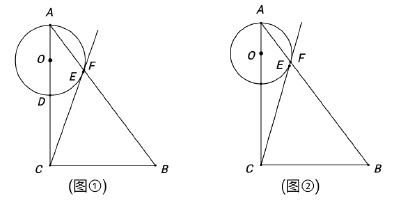
ЃЈ3ЃЉШчЭМЂкЃЌШє![]() ЃЌЕу
ЃЌЕу![]() Йигк
Йигк![]() ЕФЖдГЦЕуЮЊЕу
ЕФЖдГЦЕуЮЊЕу![]() ЃЌЪдЧѓ
ЃЌЪдЧѓ![]() ЁЂ
ЁЂ![]() СНЕужЎМфЕФОрРы.
СНЕужЎМфЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌ2ЗжБ№ЪЧФГПюРКЧђМмЕФЪЕЮяЭМгыЪОвтЭМЃЌвбжЊЕззљBC=0.60УзЃЌЕззљBCгыжЇМмACЫљГЩЕФНЧЁЯACB=75ЁуЃЌжЇМмAFЕФГЄЮЊ2.50УзЃЌРКАхЖЅЖЫFЕуЕНРКПђDЕФОрРыFD=1.35УзЃЌРКАхЕзВПжЇМмHEгыжЇМмAFЫљГЩЕФНЧЁЯFHE=60ЁуЃЌЧѓРКПђDЕНЕиУцЕФОрРыЃЈОЋШЗЕН0.01УзЃЉЃЈВЮПМЪ§ОнЃКcos75ЁуЁж0.2588ЃЌsin75ЁуЁж0.9659ЃЌtan75ЁуЁж3.732ЃЌ![]() Ёж1.732ЃЌ
Ёж1.732ЃЌ![]() Ёж1.414ЃЉ
Ёж1.414ЃЉ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com