
 的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
 ,OC=1,则OA=2;
,OC=1,则OA=2;
 ;
; ;(3分)
;(3分) =
= ,
,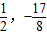 ).(4分)
).(4分)
 ,
,

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:2011-2012学年江苏省苏州市九年级(上)期末数学模拟试卷(解析版) 题型:解答题
 的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(27):20.5 二次函数的一些应用(解析版) 题型:解答题
 的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(28):2.4 二次函数的应用(解析版) 题型:解答题
 的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
查看答案和解析>>
科目:初中数学 来源:2012浙江省温州市瑞安市中考适应性考试数学试卷(解析版) 题型:解答题
 的等腰Rt△ABC(∠C=90°)放在平面直角坐标系中的第二象限,使点C的坐标为(-1,0),点A在y轴上,点B在抛物线y=ax2+ax-2上.
的等腰Rt△ABC(∠C=90°)放在平面直角坐标系中的第二象限,使点C的坐标为(-1,0),点A在y轴上,点B在抛物线y=ax2+ax-2上.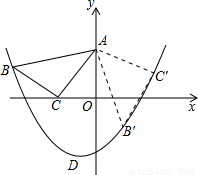
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com