
| A. | 12 | B. | 12或15 | C. | 15 | D. | 无法确定 |
分析 利用因式分解法解方程得到x1=3,x2=6,再分类讨论:当腰为6,底为3时,易得三角形周长为15;当腰为3,底为6时,根据三角形三边的关系舍去.
解答 解:(x-3)(x-6)=0,
x-3=0或x-6=0,
所以x1=3,x2=6,
当腰为6,底为3时,这个等腰三角形的周长=6+6+3=15;
当腰为3,底为6时,3+3=6,不符合三角形三边的关系,舍去,
所以这个等腰三角形的周长为15.
故选C.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了三角形三边的关系.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
 已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)
已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
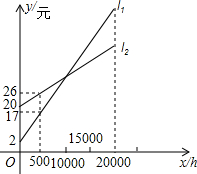 如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,
如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2014个 | B. | 2015个 | C. | 4028个 | D. | 6042个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)(a-b)=a2-b2 | B. | 2(2a-b)=4a-b | C. | 2a+3b=5ab | D. | (a+b)2=a2+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,P为AB上一点,则下列四个条件中
如图,在△ABC中,P为AB上一点,则下列四个条件中查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2ab+1)厘米 | B. | 8a2b厘米 | C. | (4ab+2)厘米 | D. | (4a2b-2a)厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
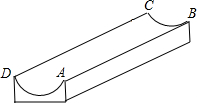 如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com