
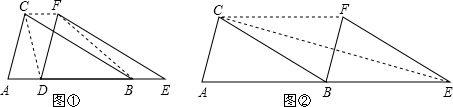
 解:(1)过点C作CE⊥AB于点H,
解:(1)过点C作CE⊥AB于点H, (CF+BD)•CH=
(CF+BD)•CH= (AD+BD)•CH=
(AD+BD)•CH= AB•CH,
AB•CH, AB•CH=3,
AB•CH=3, CB,
CB, AB,
AB, AB•CG=
AB•CG= AB2=3,
AB2=3, .
. (CF+BD)•CH=
(CF+BD)•CH= (AD+BD)•CH=
(AD+BD)•CH= AB•CH=S△ABC=3;
AB•CH=S△ABC=3; CB=
CB= AB,又由△ABC的面积为3,即可求得AB的长.
AB,又由△ABC的面积为3,即可求得AB的长.

 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
 11、如图所示,四边形ABCD是平行四边形,那么下列说法正确的有( )
11、如图所示,四边形ABCD是平行四边形,那么下列说法正确的有( )查看答案和解析>>
科目:初中数学 来源: 题型:
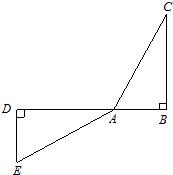 15、两个全等的三角形如下图所示放置,点B、A、D在同一直线上.操作:在图中,在CB边上截取CM=AB,连接DM,交AC于N.请探究∠AND的大小,并证明你的结论.
15、两个全等的三角形如下图所示放置,点B、A、D在同一直线上.操作:在图中,在CB边上截取CM=AB,连接DM,交AC于N.请探究∠AND的大小,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:
 明理由;它们能够由其中一个通过旋转而得到另外一个吗?简述旋转过程.
明理由;它们能够由其中一个通过旋转而得到另外一个吗?简述旋转过程.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.
如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com