
����Ŀ����ͼ��ʾ����ABC�У���B=90�㣬AB=6cm��BC=8cm��
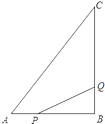
��1���� P�ӵ�A��ʼ��AB����B��1cm/s���ٶ��ƶ�����Q��B�㿪ʼ��BC�����C��2cm/s���ٶ��ƶ������P��Q�ֱ��A��Bͬʱ�������߶�PQ�ܷ���ABC�ֳ������ȵ������֣����ܣ�����˶�ʱ�䣻������˵�����ɣ�
��2����P��������AB�����A�������1cm/s���ٶ��ƶ����� Q������ CB�����C�������2cm/s���ٶ��ƶ���P��Qͬʱ�������ʼ������PBQ�����Ϊ1cm2��
���𰸡���1�����ܣ���2��5��![]() �롢5���5+
�롢5���5+![]() ��.
��.
��������
(1)�辭��x�룬�߶�PQ�ܽ���ABC�ֳ������ȵ������֣��г�������⼴�ɣ�
(2)������������ٵ�P���߶�AB�ϣ���Q���߶�CB�ϣ�0��t��4�����ڵ�P���߶�AB�ϣ���Q���߶�CB���ӳ�������4��t��6��������P���߶�AB���ӳ����ϣ���Q���߶�CB���ӳ�������t>6�����������ۼ������.
�⣺��1���辭��x�룬�߶�PQ�ܽ���ABC�ֳ������ȵ�������
������֪��AP=x��BQ=2x����BP=6��x��
�� ![]() (6��x)2x=
(6��x)2x=![]() ��
��![]() ��6��8��
��6��8��
��x2��6x+12=0��
��b2��4ac��0��
�˷����⣬
���߶�PQ���ܽ���ABC�ֳ������ȵ������֣�
��2����t���PBQ�����Ϊ1��������������ۣ�
�ٵ���P���߶�AB�ϣ���Q���߶�CB��ʱ����ʱ0��t��4��
������֪��![]() (6��t)(8��2t)=1�������ã�t2��10t+23=0����ã�t1=5+
(6��t)(8��2t)=1�������ã�t2��10t+23=0����ã�t1=5+![]() ���������⣬Ӧ��ȥ����t2=5��
���������⣬Ӧ��ȥ����t2=5��![]() ��
��
�ڵ���P���߶�AB�ϣ���Q���߶�CB���ӳ�����ʱ����ʱ4��t��6��������֪��![]() (6��t)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=t2=5��
(6��t)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=t2=5��
�۵���P���߶�AB���ӳ����ϣ���Q���߶�CB���ӳ�����ʱ����ʱt��6��������֪�� ![]() (t��6)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=5+
(t��6)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=5+![]() ��t2=5-
��t2=5-![]() ���������⣬Ӧ��ȥ����
���������⣬Ӧ��ȥ����
��������������5-![]() �롢5���5+
�롢5���5+![]() ���PBQ�����Ϊ1cm2.
���PBQ�����Ϊ1cm2.
�ʴ�Ϊ����1�����ܣ���2��5��![]() �롢5���5+
�롢5���5+![]() ��.
��.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
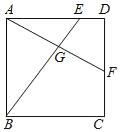
����Ŀ����ͼ��������ABCD�У�E��F�ֱ��ڱ�AD��CD�ϣ�AF��BE�ཻ�ڵ�G����AE=3ED��DF=CF����![]() ��ֵ�ǣ�������
��ֵ�ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
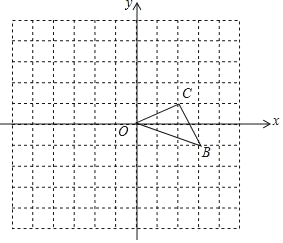
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���B������Ϊ��3����1����
(1)�Ե�OΪλ�����ģ���y�����ཫ��OBC�Ŵ�ԭ��������������ͼ��ԭͼ�����Ʊ�Ϊ2���������Ŵ��ġ�OB��C�䣻
(2)��(1)�Ļ�����д����B�䣬C�������ꣻ
(3)��(1)�Ļ����ϣ������OBC�ڲ�һ��M������Ϊ��a��b������д��M�Ķ�Ӧ��M�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
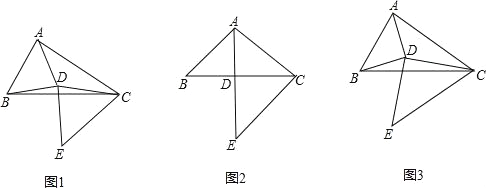
����Ŀ����ͼ1������ABC�У�BC=4�����߶�ABΪ������ABD��ʹ��AD=BD������DC������DCΪ������CDE��ʹ��DC=DE����CDE=��ADB=����
��1����ͼ2������ABC=45������=90��ʱ���õ�ʽ��ʾ�߶�AD��DE֮���������ϵ��
��2�����߶�CB��������CE�ķ���ƽ�ƣ��õ��߶�EF������BF��AF��
������=90���������ⲹȫͼ3�����߶�AF�ij���
����ֱ��д���߶�AF�ij����ú�����ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪![]() ABC���������������ֱ�ΪA����1,1����B����3,1����C����1,4����
ABC���������������ֱ�ΪA����1,1����B����3,1����C����1,4����
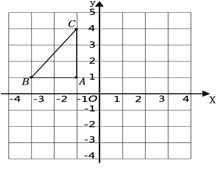
��1��������ABC����y��ԳƵ�ͼ�Σ�
��2������ABC���ŵ�B˳ʱ����ת90����õ���A2BC2������ͼ�л�����A2BC2��������߶�BC��ת��������ɨ����������������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij������ˮ�۸������(����)��(��λ��Ԫ/������)
��ˮ��� | ����ˮ�� | �����ˮ�� |
һ������������ˮ | 0.72 | |
1��һ��һ�� | ||
��һ���ݣ�����ˮ��0��30������/�� | 0.82 | |
�ڶ����ݣ�����ˮ������30������/������ | 1.23 |
�����ˮ�ۺ�ij����������ˮ��x(������)��Ӧ��ˮ��y(Ԫ)�ĺ���ͼ����(����)
A.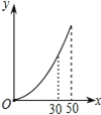 B.
B. C.
C.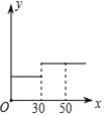 D.
D.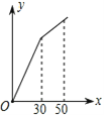
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
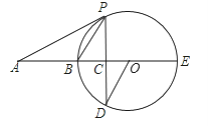
����Ŀ����ͼ��BE��ԲO��ֱ����A��EB���ӳ����ϣ�APΪԲO�����ߣ�PΪ�е㣬��PD��ֱ��BE�ڵ�C��
��1����֤����AOD=��APC��
��2����OC��CB=1��2��AB=6����ԲO�İ뾶��tan��APB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ����зֱ��ע2��4��6��3��С��С������ֲ�ͬ�⣬�����ͬ��������3�ű�����ȫһ��������ֱ�д������6��7��8�Ŀ�Ƭ���ִӿڴ�����������һ��С���ٴ���3�ű��泯�ϵĿ�Ƭ����������һ�ſ�Ƭ��
��1���������б�����״ͼ�ķ�������ʾ�����п��ܳ��ֵĽ����
��2��С���С������Ϸ���ƶ���������Ϸ����
����1�����������������֣�������һ���ǡ�6����С��Ӯ������С��Ӯ��
����2���������Ŀ�Ƭ�ϵ��������������ֵ�������ʱ��С��Ӯ������С��Ӯ��
С��Ҫ������Ϸ�л�ʤ������ѡ����һ�ֹ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
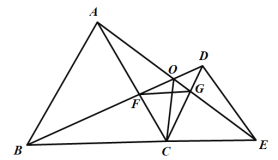
����Ŀ����ͼ����֪![]() ��
��![]() ���ǵȱ������Σ���
���ǵȱ������Σ���![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�ĸ����ǣ� ��
��������ȷ�ĸ����ǣ� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com