
【题目】如图,以![]() 的三边为边分别向三角形外作正方形
的三边为边分别向三角形外作正方形![]() 、
、![]() 、
、![]() .连结
.连结![]() 、
、![]() 、
、![]() .若
.若![]() 的面积是
的面积是![]() ,则以线段
,则以线段![]() 、
、![]() 、
、![]() 为边的三角形的面积是__________.
为边的三角形的面积是__________.

【答案】![]()
【解析】
可以利用正方形的对边平行且相等,作出一个以EF、GH、KD为边的三角形,即把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,因此可拼成一个三角形,然后再把△GCH绕C点顺时针旋转90°,得到△BCG′,可得A,C,G′在一条直线上,且C为AG′的中点,进而可得由线段![]() 、
、![]() 、
、![]() 为三边构成的△DIK的面积S△DIK=3S△ABC.
为三边构成的△DIK的面积S△DIK=3S△ABC.
解:把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,连接DI,BI,KI,

∴△DBI≌△EAF,△BIK≌△CGH,
把△GCH绕C点顺时针旋转90°,得到△BCG′,
可得A,C,G′在一条直线上,且C为AG′的中点,
所以S△BCG′=S△ABC,因此S△BIK=S△ABC,同理可得S△DBK=S△DBI=S△ABC,
因此以线段![]() 、
、![]() 、
、![]() 为三边构成的△DIK的面积S△DIK=3S△ABC=
为三边构成的△DIK的面积S△DIK=3S△ABC=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题发现:学完四边形的有关知识后,创新小组的同学进一步研究特殊的四边形,发现了一个结论.如图1,已知四边形![]() 是正方形,根据勾股定理和正方形的性质,很容易能够证明
是正方形,根据勾股定理和正方形的性质,很容易能够证明![]() .
.
问题探究:
(1)如图2,已知四边形![]() 是矩形,若
是矩形,若![]() ,则
,则![]() 的值是 ;
的值是 ;![]() 的值是 ;
的值是 ;
(2)如图3,已知四边形![]() 是菱形,证明:
是菱形,证明:![]() ;
;
拓广探索:
(3)智慧小组看了创新小组交流后,提出了一个猜想,如图4,在![]() 中,
中,![]() ,你认为这个猜想正确吗?请说明理由;
,你认为这个猜想正确吗?请说明理由;
(4)请用文字语言叙述![]() 中得出的结论.
中得出的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
![]() ;
; ![]() ;
; ![]() ;
;
(3)求出△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图一,在△ABC中,AD是角平分线,AE是高,∠ABC=30°,∠ACB=70°.
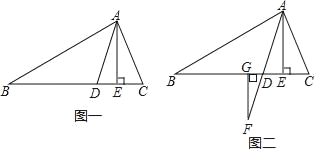
(1)求∠DAE的度数.
(2)如图二,若点F为AD延长线上一点,过点F作FG⊥BC于点G,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程.
如图,已知,∠1+∠2=180°,∠A=∠D.求证AB∥CD.
证明:∵∠1+∠2=180°(已知)
∠1=∠3( )
∴∠3+∠2=180°( )
∴AE∥ ( )
∴∠D= ( )
∵∠A=∠D(已知)
∴∠A=∠CEA( )
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届全国青年运动会(简称:二青会)将于2019年8月在山西太原开幕,甲、乙两名自行车运动员正在积极备战.如图是教练员记录的甲、乙两选手在骑车时,在某时段速度随时间变化的图象,下列结论错误的是( )
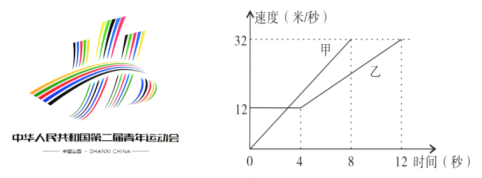
A.乙前![]() 秒行驶的路程为
秒行驶的路程为![]() 米
米
B.在![]() 到
到![]() 秒内甲的速度每秒增加
秒内甲的速度每秒增加![]() 米/秒
米/秒
C.甲、乙到第![]() 秒时行驶的路程相等
秒时行驶的路程相等
D.在![]() 至
至![]() 秒内甲的速度都大于乙的速度
秒内甲的速度都大于乙的速度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com