
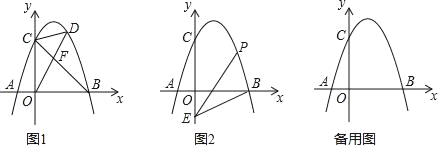
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)点D的坐标为(1,4)或(2,3);(3)点P坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)OB=OC=3,则:B(3,0),C(0,-3),把B、C坐标代入抛物线方程,解得抛物线方程为:y=-x2+2x+3;
(2)S△COF:S△CDF=3:2,则S△COF=![]() S△COD,即:xD=
S△COD,即:xD=![]() xF,即可求解;
xF,即可求解;
(3)分∠PBE或∠PEB等于2∠OBE两种情况分别求解即可.
(1)OB=OC=3,则:B(3,0),C(0,﹣3),
把B、C坐标代入抛物线方程,
解得抛物线方程为:y=﹣x2+2x+3;
(2)∵S△COF:S△CDF=3:2,
∴S△COF=![]() S△COD,即:xD=
S△COD,即:xD=![]() xF,
xF,
设:F点横坐标为3t,则D点横坐标为5t,
点F在直线BC上,
而BC所在的直线方程为:y=﹣x+3,则F(3t,3﹣3t),
则:直线OF所在的直线方程为:y=![]() x=
x=![]() x,
x,
则点D(5t,5﹣5t),
把D点坐标代入①,解得:t=![]() 或
或![]() ,
,
则点D的坐标为(1,4)或(2,3);
(3)①如图所示,当∠PEB=2∠OBE=2α时,
过点E作∠PEB的平分线交x轴于G点,PE交x轴于H点,
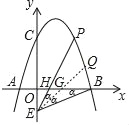
则:∠PEQ=∠QEB=∠ABE=α,则∠HGE=2α,
设:GB=m,则:OG=3﹣m,GE=m,
在Rt△OGE中,由勾股定理得:EG2=OG2+OE2,
即:m2=(3﹣m)2+(![]() )2,解得:m=
)2,解得:m=![]() ,
,
则:GE=![]() ,OG=
,OG=![]() ,BE=
,BE=![]() ,
,
∵∠PEQ=∠ABE=α,∠EHG=∠EHG,∴△HGE∽△HEB,
∴![]() =
=![]() =
=![]() ,设:GH=
,设:GH=![]() x,HE=4x,
x,HE=4x,
在Rt△OHE中,OH=OG﹣HG=![]() ﹣
﹣![]() x,OE=
x,OE=![]() ,EH=4x,
,EH=4x,
由勾股定理解得:x=![]() ,则:OH=
,则:OH=![]() ,H(
,H(![]() ,0),
,0),
把E、H两点坐标代入一次函数表达式,
解得EH所在直线的表达式为:y=![]() x﹣
x﹣![]() ,
,
将上式与①联立并解得:x=![]() ,
,
则点P(![]() ,
,![]() );
);
②当∠PBE=2∠OBE时,则∠PBO=∠EBO,
BE所在直线的k值为![]() ,则BE所在直线的k值为﹣
,则BE所在直线的k值为﹣![]() ,
,
则:PB所在的直线方程为:y=﹣![]() x+3,
x+3,
将上式与①联立,解得:x=![]() ,(x=0已舍去),
,(x=0已舍去),
则点P(![]() ,
,![]() ),
),
故:点P坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】若|m+3|+![]() =0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
=0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
A. y=![]() (x﹣3)2+2B. y=
(x﹣3)2+2B. y=![]() (x+3)2﹣2
(x+3)2﹣2
C. y=![]() (x﹣3)2﹣2D. y=
(x﹣3)2﹣2D. y=![]() (x+3)2+2
(x+3)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
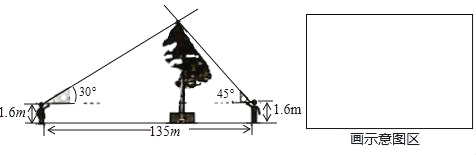
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.
(1)请在指定区域内画出小红和小阳测量古松树高的示意图;
(2)通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
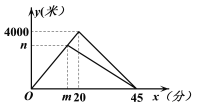
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;
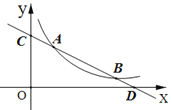
(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
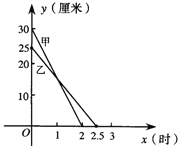
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽甲所用的时间为 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,且CD2=ADDB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DFDC.则下列结论正确的是( )
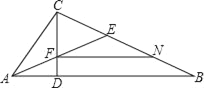
A. ①②④ B. ②③④ C. ①②③④ D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com