
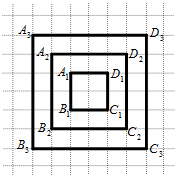
 16、正方形网格中,每个小格的顶点叫做格点.当所作正方形边上的点刚好在格点上的点称为整点.如图中A1B1C1D1四条边上的整点共有8个;A2B2C2D2四条边上的整点共有16个.请你观察图中正方形A3B3C3D3四条边上的整点的个数…按此规律,推算出正方形A10B10C10D10四条边上的整点共有
16、正方形网格中,每个小格的顶点叫做格点.当所作正方形边上的点刚好在格点上的点称为整点.如图中A1B1C1D1四条边上的整点共有8个;A2B2C2D2四条边上的整点共有16个.请你观察图中正方形A3B3C3D3四条边上的整点的个数…按此规律,推算出正方形A10B10C10D10四条边上的整点共有


科目:初中数学 来源: 题型:
 12、如图是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),如果分别用(3,1),(3,5)表示图中图书馆和教学楼的位置,那么实验楼的位置应表示为
12、如图是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),如果分别用(3,1),(3,5)表示图中图书馆和教学楼的位置,那么实验楼的位置应表示为查看答案和解析>>
科目:初中数学 来源: 题型:
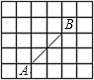 分析,探究回答下列问题:
分析,探究回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 13 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com