
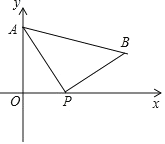
����Ŀ����ͼ��A��0��4����ֱ������ϵ y ����һ�㣬���� P ��ԭ�� O �������� x ���������˶����ٶ�Ϊÿ�� 1 ����λ���ȣ���PΪֱ�Ƕ����ڵ�һ������������Rt��APB����P����˶�ʱ��Ϊ t �룮
��1���� AB��x �ᣬ�� t ��ֵ��
��2����OP=![]() OA����B������꣮
OA����B������꣮
��3���� t=3 ʱ��x �����Ƿ������һ�� M��ʹ���� M��P��A Ϊ������������ǵ��������Σ���ֱ��д���� M �����꣮
���𰸡���1��4����2���� B ������Ϊ��6��2������3��������.
��������
�� AB��x �ᣬ���ҳ��ı��� ABCO Ϊ�����Σ��ٸ�����APB Ϊ���������οɵ�֪��OAP=45�����Ӷ��ó���AOP Ϊ����ֱ�������Σ��ɴ˵ó����ۣ�
�� BQ��x ���ڵ� Q��֤��OAP�ա�QPB �� BQ=OP=![]() OA=2��PQ=AO=4���ݴ�֪ OQ=OP+PQ=6���Ӷ��ó��𰸣�
OA=2��PQ=AO=4���ݴ�֪ OQ=OP+PQ=6���Ӷ��ó��𰸣�
��� M��x��0����֪ MA=![]() ��MP=|x-3|���ٷ� MA=MP��MA=AP�� AP=MP ����������ɵã�
��MP=|x-3|���ٷ� MA=MP��MA=AP�� AP=MP ����������ɵã�
�⣺��1������ B �� BC��x ���ڵ� C����ͼ 1 ��ʾ��
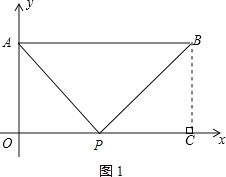
��AO��x �ᣬBC��x �ᣬ�� AB��x �ᣬ
���ı��� ABCO Ϊ�����Σ�
��AO=BC=4��
�ߡ�APB Ϊ����ֱ�������Σ�
��AP=BP����PAB=��PBA=45�㣬
���OAP=90��-��PAB=45�㣬
���AOP Ϊ����ֱ�������Σ�
��OA=OP=4��
t=4��1=4 ���룩�� �� t ��ֵΪ 4��
��2����ͼ 2������ B �� BQ��x ���ڵ� Q��
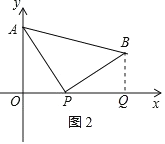
���AOP=��BQP=90�㣬
���OAP+��OPA=90�㣬
�ߡ�ABP Ϊ����ֱ�������Σ�
��PA=PB����APB=90�㣬
���AOP+��BPQ=90�㣬
���OAP=��QPB��
���OAP�ա�QPB��AAS����
�� BQ=OP=![]() OA=2��PQ=AO=4��
OA=2��PQ=AO=4��
�� OQ=OP+PQ=6��
��� B ��������6��2����
��3���� t=3 ʱ���� OP=3��
��OA=4��
��AP=5��
��� M��x��0����
�� MA=![]() =
=![]() ��MP=|x-3|��
��MP=|x-3|��
�ٵ� MA=MP ʱ��![]() =|x-3|�����
=|x-3|�����
x=-![]() ��
��
�ڵ� MA=AP ʱ��![]() =5����� x=-3 �� x=3���ᣩ��
=5����� x=-3 �� x=3���ᣩ��
�۵� AP=MP ʱ��|x-3|=5����ã�x=8 �� x=-2��
���ϣ��� M ������Ϊ��![]() ��0����-3��0����8��0����-2��0��
��0����-3��0����8��0����-2��0��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
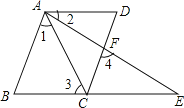
����Ŀ����ͼ���ڡ�ABC �У���C=90�㣬��A=34�㣬D��E �ֱ�Ϊ AB��AC ��һ�㣬����BCD����ADE �� CD��DE �������� A��B ǡ���غ��ڵ� P �������ACP=_______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB��CD����1=��2����3=��4��
��1����֤��AD��BE��
��2������B=��3=2��2�����D�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʮ��������ʿ��ѧ��ŷ��֤���˼������ж�����(V)������(F)������(E)֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������Ϊŷ����ʽ������۲����м��ּĶ�����ģ�ͣ�����������⣺
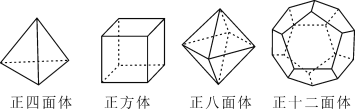
(1)��������Ķ�����ģ�ͣ���ɱ���
������ | ������(V) | ����(F) | ����(E) |
������ | 4 | 4 | |
������ | 8 | 12 | |
�������� | 6 | 8 | 12 |
��ʮ������ | 20 | 12 | 30 |
���Է��ֶ�����(V)������(F)������(E)֮����ڵĹ�ϵʽ��_______________��
(2)��һ��������������ȶ�������8������30���⣬������������������______��
(3)ij��������Ʒ�������Ǽ����壬������������������κͰ˱������ֶ����ƴ�Ӷ��ɣ�����24�����㣬ÿ�����㴦��3���⣮��ö���������������εĸ���Ϊx���˱��εĸ���Ϊy����x��y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����BAC��90������D��ֱ��AB�ϵ�һ���㣨����A��B�غϣ���BE��CD��E����ֱ��AC��F��
��1����D�ڱ�AB��ʱ����֤����BD��AB��AF��
��2����̽������D��AB���ӳ������ӳ�����ʱ�����ڱ���ͼ�л���ͼ�Σ���1���еĽ����Ƿ������������������ֱ��д����ȷ���ۣ�����Ҫ֤������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ
��1��[��x��y��2+��x+y����x��y��]��2x������x=3��y=1.5
��2����![]() +m��2����
+m��2����![]() ������m=��
������m=��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1�� ![]() �������B������Ϊ�� ��
�������B�������� �� 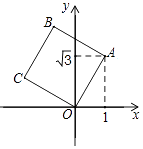
A.��1�� ![]() ��
�� ![]() +1��
+1��
B.���� ![]() ��
�� ![]() +1��??
+1��??
C.����1�� ![]() +1��
+1��
D.����1�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е���ABC����С����߳�Ϊ1�������ABC�������������߽���������Σ��Ķ���A��C������ֱ�Ϊ����1��1������0����2�������������ѧ��֪ʶ��
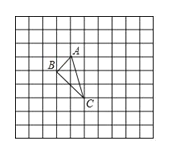
��1������ͼ��ʾ������ƽ��������ƽ��ֱ������ϵ��
��2��������ABC����y��ԳƵ�������A1B1C1��
��3���ж���ABC����״���������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ�ۺ�ʵ��С���ͬѧ�ԡ���ɫ���С�Ϊ���⣬��ijС���ľ���Թ����������˽��ʹ������������ʾ����飬����ε����У�������20�˶��ڹ����������˽⣬ʹ�ù��������ľ���ÿ������·�̲�����8ǧ�ף�����������������ͳ��ͼ����ͼ��ʾ�� 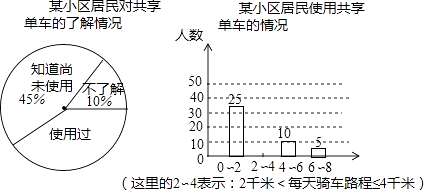
��1�����ε����������� �� ʹ�ù�����������������
��2���뽫����ͳ��ͼ����������
��3��������С����Լ��3000������������ÿ�������·����2��4ǧ���ж����ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com