
 朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题.
朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题. | 频数 | 频率 | |
| 60<x≤72 | 2 | 0.04 |
| 72<x≤84 | 8 | 0.16 |
| 84<x≤96 | 20 | a |
| 96<x≤108 | 16 | 0.32 |
| 108<x≤120 | b | 0.08 |
| 合计 | 50 | 1 |
分析 (1)根据频率之和为1与频数之和等于50分别列式计算即可求出a、b;
(2)根据b的值补全统计图即可;
(3)设另外两个人分别是A、B,然后画出树状图,再根据概率公式进行计算即可得解.
解答  解:(1)a=1-0.04-0.16-0.32-0.08=1-0.6=0.4,
解:(1)a=1-0.04-0.16-0.32-0.08=1-0.6=0.4,
b=50-2-8-20-16=50-46=4;
故答案为:0.4,4;
(2)补全统计图如图所示;
(3)设另外两个人分别是A、B,
根据题意画出树状图如下:
所有可能出现的结果是:(小明,小红),(小明、A),(小明,B),(小红,小明),(小红,A),(小红,B),(A,小明),(A,小红),(A,B),(B,小明),(B,小红),(B,A),
由此可见,共有12种可能出现的结果,这些结果出现的可能性相等,其中抽到小明、小红两名学生的结果有2种,所以,P(恰好抽到小明,小红)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | A1(-2,-1),B1(2,1),C1(1,-4) | B. | A1(-1,1),B1(3,3),C1(2,-2) | ||
| C. | A1(0,0),B1(4,2),C1(3,-3) | D. | A1(-1,2),B1(3,4),C1(2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
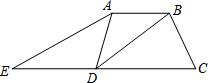 如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.
如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com