
【题目】 请将下列证明过程补充完整:
已知:∠1=∠E,∠B=∠D.求证:AB∥CD
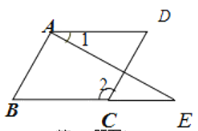
证明:∵ ∠1=∠E( 已知 )
∴ ∥ ( )
∴ ∠D+∠2=180° ( )
∵ ∠B=∠D( 已知 )
∴ ∠B+ ∠2= 180° ( )
∴ AB∥CD ( )
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】关于x的方程 ![]() 有两个不相等的实数根,
有两个不相等的实数根,
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD= 120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 . 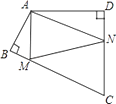
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
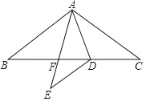
【题目】如图,在△ABC中,点D在BC上,AB=AC=BD,AD=DC,将△ACD沿AD折叠至△AED,AE交BC于点F.
(1)求∠C的度数;
(2)求证:BF=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
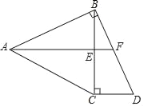
【题目】如图,在等腰△ABC中,AB=AC,过点B作BD⊥AB,过点C作CD⊥BC,两线相交于点D,AF平分∠BAC交BC于点E,交BD于点F.
(1)若∠BAC=68°,求∠DBC;
(2)求证:点F为BD中点;
(3)若AC=BD,且CD=3,求四边形ABDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.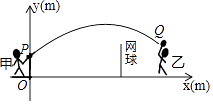
(1)当a=﹣ ![]() 时,①求h的值;
时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A、B表示的点分别为-6和3
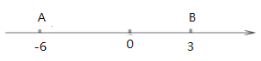
(1)若数轴上有一点P,它到A和点B的距离相等,则点P对应的数字是________(直接写出答案)
(2)在上问的情况下,动点Q从点P出发,以3个单位长度/秒的速度在数轴上向左移动,是否存在某一个时刻,Q点与B点的距离等于 Q点与A点的距离的2倍?若存在,求出点Q运动的时间,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com