
在四边形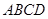 中,对角线
中,对角线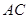 平分
平分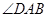 .
.
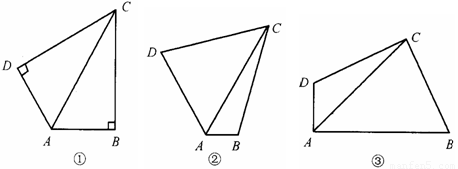
(1)如图①,当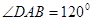 ,
,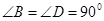 时,求证:
时,求证: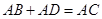 ;
;
(2)如图②,当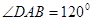 ,
,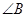 与
与 互补时,线段
互补时,线段 有怎样的数量关系?写出你的猜想,并给予证明;
有怎样的数量关系?写出你的猜想,并给予证明;
(3)如图③,当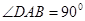 ,
,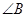 与
与 互补时,线段
互补时,线段 有怎样的数量关系?直接写出你的猜想.
有怎样的数量关系?直接写出你的猜想.
(1)在四边形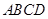 中,由
中,由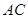 平分
平分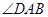 ,
,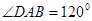
可得 ,又
,又 ,
,
可得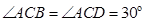 ,
,
根据含30°角的直角三角形的性质可得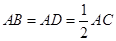 ,即可得到结论;
,即可得到结论;
(2)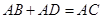 ;
;
(3)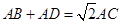
【解析】
试题分析:(1)在四边形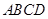 中,由
中,由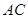 平分
平分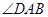 ,
,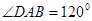 可得
可得 ,又
,又 ,可得
,可得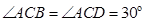 ,根据含30°角的直角三角形的性质可得
,根据含30°角的直角三角形的性质可得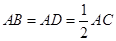 ,即可得到结论;
,即可得到结论;
(2)过 点分别作CE⊥
点分别作CE⊥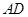 于E,CF⊥
于E,CF⊥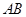 交AB延长线于F,根据角平分线的性质可得CE=CF,由
交AB延长线于F,根据角平分线的性质可得CE=CF,由
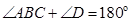 ,
,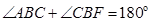 可得
可得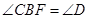 ,再结合
,再结合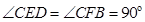 可证得
可证得 ≌
≌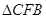 ,即得
,即得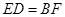 ,再结合(1)中
,再结合(1)中 即可求得结果;
即可求得结果;
(3)解法同(2).
解:(1)在四边形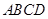 中,
中,
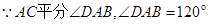 ,
,
∴ .
.
又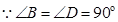 ,
,
∴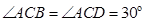 .
.
∴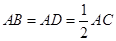 .
.
即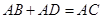 ;
;
(2)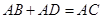 .
.
证明如下:如图,过 点分别作CE⊥
点分别作CE⊥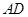 于E,CF⊥
于E,CF⊥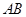 交AB延长线于F,
交AB延长线于F,
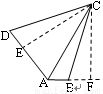


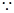
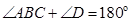 ,
,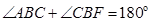
∴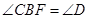
∵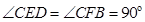
∴ ≌
≌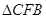
∴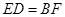
∴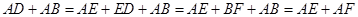 .
.
由(1)知 .
.
∴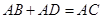 ;
;
(3)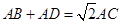 .
.
考点:角平分线的性质,全等三角形的判定和性质
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 (2014•宁波一模)如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )
(2014•宁波一模)如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )查看答案和解析>>
科目:初中数学 来源: 题型:022
在平形四边形ABCD中.对角线AC和BD相交于点O.
(1)如果∠ABO+∠ADO=90°,那么平形四边形ABCD是________形;
(2)如果∠AOB=∠AOD,那么平形四边形ABCD是_________形;
(3)如果AB=BC,AC=BD,那么平形四边形ABCD是________形.
查看答案和解析>>
科目:初中数学 来源:2013届浙江省杭州市江南实验学校九年级5月月考数学试卷(带解析) 题型:单选题
如图,在正方形ABCD中,对角线AC,BD交于点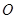 ,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③
,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③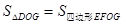 ;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。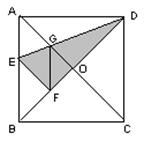
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省九年级5月月考数学试卷(解析版) 题型:选择题
如图,在正方形ABCD中,对角线AC,BD交于点 ,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③
,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③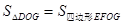 ;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
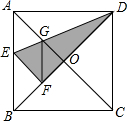 如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为
如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com