
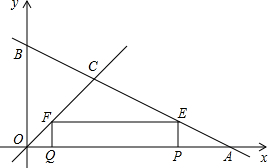
 如图所示,直线y=-$\frac{1}{2}x$+4与坐标轴分别交于点A、B,与直线y=x交于点C,在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形总为矩形(点P、Q重合除外).
如图所示,直线y=-$\frac{1}{2}x$+4与坐标轴分别交于点A、B,与直线y=x交于点C,在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形总为矩形(点P、Q重合除外).分析 (1)根据直线y=-$\frac{1}{2}$x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出$\frac{OB}{AO}$=$\frac{EP}{AP}$=$\frac{1}{2}$,据此可以求得点P的运动速度;
(2)先求得矩形PEFQ的面积s与t的函数关系式,进而根据等量关系:矩形PEFQ的面积为5,列出方程求解即可.
解答 解:(1)∵直线y=-$\frac{1}{2}$x+4与坐标轴分别交于点A、B,
∴x=0时,y=4,y=0时,x=8,
∴$\frac{OB}{AO}$=$\frac{4}{8}$=$\frac{1}{2}$,
当t秒时,QO=FQ=t,则EP=t,
∵EP∥BO,
∴$\frac{OB}{AO}$=$\frac{EP}{AP}$=$\frac{1}{2}$,
∴AP=2t,
∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,
∴点P运动的速度是每秒2个单位长度;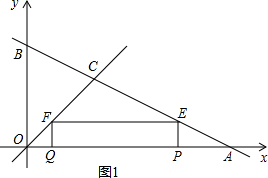 (2)如图1,当Q在P点的左边时,
(2)如图1,当Q在P点的左边时,
∵OQ=t,PA=2t,
∴QP=8-t-2t=8-3t,
∴S矩形PEFQ=QP•QF=(8-3t)•t=8t-3t2,
依题意有
8t-3t2=5,
解得t1=1,t2=$\frac{5}{3}$;
如图2,当Q在P点的右边时, ∵OQ=t,PA=2t,
∵OQ=t,PA=2t,
∴2t>8-t,
∴t>$\frac{8}{3}$,
∴QP=t-(8-2t)=3t-8,
∴S矩形PEFQ=QP•QF=(3t-8)•t=3t2-8t,
∵当点P、Q其中一点停止运动时,另一点也停止运动,
∴$\frac{8}{3}$<t≤4,
依题意有
3t2-8t=5,
解得t3=$\frac{4-\sqrt{31}}{3}$(不合题意舍去),t4=$\frac{4+\sqrt{31}}{3}$;
综上所述,当t=1或$\frac{5}{3}$或$\frac{4+\sqrt{31}}{3}$时,矩形PEFQ的面积为5.
点评 此题主要考查了二次函数与一次函数的综合应用,得出P,Q不同的位置进行分类讨论得出是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.
如图所示,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
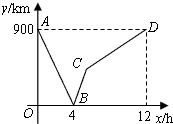 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
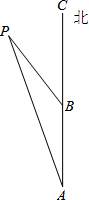 如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围18海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围18海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com