
分析 利用两组对应值得到两个关于a、b、c的方程,再利用抛物线与x轴两交点间的距离公式得到第三个关于a、b、c的方程,于是得到关于a、b、c的方程组,然后解方程组求出a、b、c的值即可确定二次函数解析式.
解答 解:根据题意得$\left\{\begin{array}{l}c=2\\ a+b+c=-1\\ \frac{\sqrt{{b}^{2}-4ab}}{\left|a\right|}=2\sqrt{2}\end{array}\right.$,
解得$\left\{\begin{array}{l}a=1\\ b=-4\\ c=2\end{array}\right.$或$\left\{\begin{array}{l}a=-\frac{9}{7}\\ b=-\frac{12}{7}\\ c=2\end{array}\right.$.
所以这个二次函数的解析式为y=x2-4x+2或y=-$\frac{9}{7}$x2-$\frac{12}{7}$x+2.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


科目:初中数学 来源: 题型:解答题
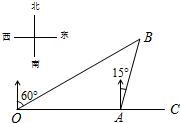 如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.
如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年度 | 2001 | 2002 | 2003 | 2004 |
| 投入技术改进资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)抛物线的顶点在原点,且经过点(-2,8),求该抛物线的解析式.
(1)抛物线的顶点在原点,且经过点(-2,8),求该抛物线的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com