
分析 (1)先对原式化简,然后将x=$\frac{1}{2}$代入化简后的式子即可解答本题;
(2)根据幂的乘方、特殊角的三角函数值和去绝对值可以解答本题.
解答 解:(1)$\frac{{x}^{2}-2x}{{x}^{2}-1}$÷(x-1-$\frac{2x-1}{x+1}$)
=$\frac{x(x-2)}{(x+1)(x-1)}÷\frac{(x-1)(x+1)-(2x-1)}{x+1}$
=$\frac{x(x-2)}{(x+1)(x-1)}×\frac{x+1}{{x}^{2}-1-2x+1}$
=$\frac{x(x-2)}{(x+1)(x-1)}×\frac{x+1}{x(x-2)}$
=$\frac{1}{x-1}$,
当x=$\frac{1}{2}$时,原式=$\frac{1}{\frac{1}{2}-1}=\frac{1}{-\frac{1}{2}}=-2$;
(2)(-2)2+2$\sqrt{12}$-8cos30°-|-3|
=4+$4\sqrt{3}$-8×$\frac{\sqrt{3}}{2}$-3
=4$+4\sqrt{3}-4\sqrt{3}-3$
=1.
点评 本题考查实数的运算、分式的化简求值、特殊角的三角函数值,解题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:解答题
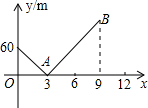 小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:
小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x2)4=x8 | B. | a6÷a2=a3 | C. | a2+a3=a5 | D. | (-a)${\;}^{-1}=\frac{1}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
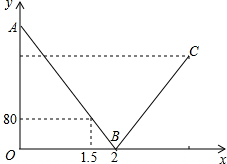 一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:
一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com