
【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.

(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
【答案】(1)平行四边形,理由见解析(2)25
【解析】
试题分析:(1)由平行线的性质得出内错角相等,由中点的定义得出AE=DE,由ASA证明△ABE≌△DFE,得出BE=FE,即可得出结论;
(2)由(1)可知△ABE≌△DFE,所以求△BCF的面积可转化为求梯形ABCD的面积,根据梯形的面积公式计算即可.
解:(1)如图所示:
四边形ABDF是平行四边形,理由如下:
∵AB∥CD,
∴∠A=∠EDF,
∵E是AD的中点,
∴AE=DE,
在△ABE和△DFE中,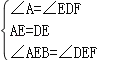 ,
,
∴△ABE≌△DFE(ASA),
∴BE=FE,
∴四边形ABDF是平行四边形;
(2)∵△ABE≌△DFE,BC⊥CD,
∴△BCF的面积=梯形ABCD的面积=![]() (AB+CD)×BC=
(AB+CD)×BC=![]() (4+6)×5=25.
(4+6)×5=25.


科目:初中数学 来源: 题型:
【题目】已知x,y,z是三个非负数,并且满足x+2y-5z=6,2x+y+5z=9.设k=3x+y+5z,记a为k的最大值,b为k的最小值,试求ab的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
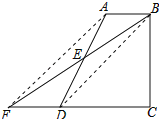
【题目】如图,将边长分别为6,2 ![]() 的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是(只填序号)
的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E,F,连接EF.
(1)求证:BC是⊙O的切线;
(2)若FC=2,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
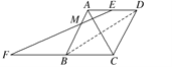
【题目】已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是![]() ,∠AEM=30°.求菱形ABCD的周长和面积.
,∠AEM=30°.求菱形ABCD的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,A(0,4),C(2,0).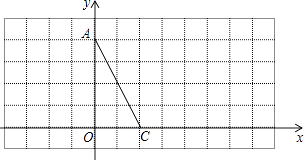
(1)画出线段AC关于y轴的对称线段AB;
(2)将线段CA绕点C顺时针旋转一个角,得到对应的线段CD,使得AD∥x轴,请画出线段CD;
(3)若直线y=kx平分四边形ABCD的面积,请求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1 , 再过点A1作x轴的垂线,垂足为点O1 , 以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017 , 则点A2017的纵坐标为( )
A.( ![]() )2017
)2017
B.( ![]() )2016
)2016
C.( ![]() )2015
)2015
D.( ![]() )2014
)2014
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.
的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.
(1)求b的值,并求出△PAB为等腰三角形时点P的坐标;
(2)在点P出发的同时,动点Q也从点A出发,以每秒![]() 个单位的速度,沿射线AB运动,运动时间为t(s);
个单位的速度,沿射线AB运动,运动时间为t(s);
①点Q的坐标(用含t的表达式表示);
②若点P的运动速度为每秒k个单位,请直接写出当△APQ为等腰三角形时k的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com