
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
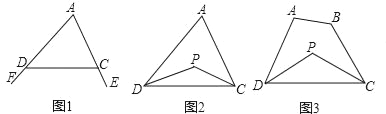
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
【答案】探究一:∠FDC+∠ECD=180°+∠A;探究二:∠P=90°+![]() ∠A;探究三:∠P=
∠A;探究三:∠P=![]() (∠A+∠B).
(∠A+∠B).
【解析】
探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;
探究二:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可.
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD
∠ACD
=180°﹣![]() (∠ADC+∠ACD)
(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD
∠BCD
=180°﹣![]() (∠ADC+∠BCD)
(∠ADC+∠BCD)
=180°﹣![]() (360°﹣∠A﹣∠B)
(360°﹣∠A﹣∠B)
=![]() (∠A+∠B).
(∠A+∠B).
故答案为:探究一:∠FDC+∠ECD=180°+∠A;探究二:∠P=90°+![]() ∠A;探究三:∠P=
∠A;探究三:∠P=![]() (∠A+∠B).
(∠A+∠B).


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
科目:初中数学 来源: 题型:
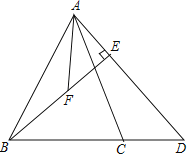
【题目】如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=![]() ,AE=
,AE=![]() ,求BE的长;
,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年汶川车厘子喜获丰收,车厘子一上市,水果店的王老板用2500元购进一批车厘子,很快售完;老板又用4400元购进第二批车厘子,所购数量是第一批的2倍,由于进货量增加,进价比第一批每干克少了3元.”
(l)第一批车厘子每千克进价多少元?.
(2)该老板在销售第二批车厘子时,售价在第二批进价的基础上增加了![]() ,售出
,售出![]() 后,为了尽快售完,决定将剩余车厘子在第二批进价的基础上每千克降价
后,为了尽快售完,决定将剩余车厘子在第二批进价的基础上每千克降价![]() 元进行促销,结果第二批车厘子的销售利润为1520元,求
元进行促销,结果第二批车厘子的销售利润为1520元,求![]() 的值。(利润=售价一进价)
的值。(利润=售价一进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张小卡片上分别写有数字1、2、3、4。它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字2的概率.
(2)随机地从盒子里抽取一张,记下数字后放回再抽取第二张。请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知![]() 是⊙
是⊙![]() 的直径,
的直径, ![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() 、
、![]() 不重合),连接
不重合),连接![]() .
. ![]() 是
是![]() 的中点,作弦
的中点,作弦![]() ,垂足为
,垂足为![]() .
.
(![]() )若点
)若点![]() 和点
和点![]() 不重合,连接
不重合,连接![]() 、
、![]() 和
和![]() .当
.当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的度数.
的度数.
(![]() )若点
)若点![]() 和点
和点![]() 重合,如图②.探索
重合,如图②.探索![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com