
 如图,将一根绳子对折以后用线段AB表示,点P是AB的四等分点,现从P处将绳子剪断,剪断后的各段绳子中的一段长为30cm,则这条绳子的原长为40或80或120或240cm.
如图,将一根绳子对折以后用线段AB表示,点P是AB的四等分点,现从P处将绳子剪断,剪断后的各段绳子中的一段长为30cm,则这条绳子的原长为40或80或120或240cm. 分析 分AP=$\frac{1}{3}$PB、PB=$\frac{1}{3}$AP这两种情况,结合图形就所得三段绳子其中一段长度为30cm,再分类讨论求解可得.
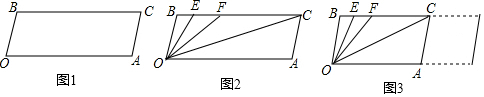
解答 解:①如图1,当AP=$\frac{1}{3}$PB时,此时剪开的三段分别为AP、PP′、A′P′,
若AP=A′P′=30cm,则PB=P′B=3PA=90cm,此时AA′=AP+PP′+A′P′=30+180+30=240(cm);
若PP′=30cm,则PB=P′B=15cm,AP=A′P′=$\frac{1}{3}$PB=5cm,此时AA′=5+30+5=40(cm);
②如图2,当PB=$\frac{1}{3}$AP时,此时剪开的三段分别为AP、PP′、A′P′,
若AP=A′P′=30cm,则PB=P′B=$\frac{1}{3}$AP=10cm,此时AA′=AP+PP′+A′P′=30+20+30=80(cm);
若PP′=30cm,则PB=P′B=15cm,AP=A′P′=3PB=45cm,此时AA′=AP+PP′+A′P′=45+30+45=120(cm),
综上,这条绳子的原长为40或80或120或240cm,
故答案为:40或80或120或240.
点评 本题主要考查两点间的距离公式,熟练掌握线段等分点的性质和线段的和差计算及分类讨论思想的运用是解题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某班学生最喜爱的体育项目 | B. | 核实某位病人血液中被感染的病毒 | ||
| C. | 了解长江中鱼的种类 | D. | 调查一批炮弹的杀伤半径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
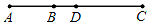 如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点.看图说话:
如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点.看图说话:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com